Coefficient de ruissellement (HU)
Traduction anglaise : Runoff coefficient
Dernière mise à jour : 18/07/2023
Coefficient traduisant le rapport entre l’une des caractéristiques de la pluie brute précipitée sur un bassin versant et l’une des caractéristiques de la pluie nette écoulée à son exutoire pendant une durée donnée.
Le concept de coefficient de ruissellement, en particulier en hydrologie urbaine, consiste à supposer qu’à l’échelle d’un élément de surface réceptrice, voire de la totalité du bassin, la pluie nette ou le ruissellement peuvent s’exprimer sous la forme d’une fraction $ C $ de la pluie brute. Cette fraction peut être relative :
- soit aux hauteurs totales de précipitation ou aux volumes mis en jeu au cours d’un événement pluvieux, on parle alors de coefficient « volumétrique » de ruissellement $ Cv $ (on parle également dans ce cas de coefficient d'écoulement ou même de coefficient d'apport) ;
- soit aux flux mis en jeu et l’on parle alors de coefficient de ruissellement « instantané » $ C(t) $.
Concepts de base
Il existe différentes façons d'exprimer le coefficient de ruissellement selon l'échelle de temps et l'échelle d'espace que l'on considère.
- pour les coefficients de ruissellement instantanés, à l'échelle d'un élément de surface on peut écrire :
- pour les coefficients de ruissellement instantanés, à l'échelle d'un bassin versant on peut écrire :
- pour les coefficients volumétriques de ruissellement, à l'échelle d'un élément de surface on peut écrire :
- pour les coefficients volumétriques de ruissellement (que l'on appelle parfois coefficients de production ou coefficients d'apport), à l'échelle d'un bassin versant on peut écrire :
Avec :
- $ i_b (x, y, t) $ : intensité de pluie brute à l'instant $ t $ au point de coordonnées $ x, y $ ;
- $ i_n (x, y, t) $ : intensité de pluie nette à l'instant $ t $ au point de coordonnées $ x, y $ ;
- $ p (x, y, t) $ : pertes au point de coordonnées $ x, y $ et au temps $ t $ ;
- $ Q_s(t) $ : débit à l'exutoire du bassin versant au temps $ t $ ;
- $ H_p(x,y) $ : hauteur totale de pertes au point de coordonnées $ x, y $ ;
- $ H_b(x,y $) : hauteur totale de pluie brute au point de coordonnées $ x, y $ ;
- $ H_n(x,y) $ : hauteur totale de pluie nette au point de coordonnées $ x, y $ ;
- $ V_b $ : volume total de pluie précipité sur la bassin versant (volume de pluie brute) ;
- $ V_s $ : volume total sortant du bassin versant pour la pluie.
Les relations entre les coefficients locaux (ou élémentaires) de ruissellement (équations $ (1) $ et $ (3) $), qui pourraient avoir un sens physique (et être localement mesurés), et les coefficients globaux, à l'échelle d'une unité hydrologique (équations $ (2) $ et $ (4) $), ne sont pas évidentes sans hypothèses particulières. En fait, la formulation des coefficients $ C_A(t) $ et $ Cv_A $, à l'échelle d'un bassin versant, est essentiellement conceptuelle, et repose sur l'hypothèse d'une analogie de comportement entre la parcelle élémentaire et la totalité du bassin versant.
Modélisation des pertes par un coefficient de ruissellement global constant
Domaine d'utilisation du modèle
Déterminer le coefficient volumétrique de ruissellement pour une pluie observée pour laquelle on dispose de mesures représentatives de la hauteur de pluie précipitée sur le bassin versant et du volume écoulé à l'exutoire est relativement simple. La difficulté consiste à prévoir la valeur à attribuer à ce coefficient pour une pluie non encore observée, en particulier si l'on s'intéresse à une autre grandeur que le volume total produit. Il existe par exemple des modèles qui utilisent cette notion pour calculer le débit maximum sortant du bassin versant (méthode rationnelle, méthode de Caquot, etc.). On peut également utiliser une fonction de production très simple pour calculer la pluie nette (ou le débit instantané de pluie nette) en fonction de l'intensité instantanée de pluie brute :
Nota : L'intensité de pluie nette, comme le débit de pluie nette obtenu en multipliant l'intensité de pluie nette par la surface du bassin versant, sont des grandeurs intermédiaires virtuelles utilisées en entrée du modèle de transfert pour calculer le débit de sortie du bassin versant.
Introduction de la notion de pertes initiales
Une amélioration simple du modèle consiste à associer au coefficient de ruissellement constant des pertes initiales $ PI_A $ qui représentent la hauteur de pluie nécessaire pour que le ruissellement puisse commencer. Ce nouveau paramètre permet de tenir compte du comportement des bassins versants pour les pluies les plus faibles. On peut alors écrire :
Soit :
Avec :
- $ Cv_A $ : coefficient volumétrique de ruissellement ;
- $ V_s $ : volume total sortant du bassin versant pour la pluie ; $ V_s=\int{Q_s(t).dt} $ (m3) ;
- $ PI_A $ : perte initiale : hauteur de pluie minimum nécessaire pour que le ruissellement commence (m) ;
- $ H_b $ : Hauteur d'eau totale moyenne précipitée sur le bassin versant (m).
Nota : En théorie on devrait calculer $ H_b $ par une relation de la forme : $ H_b = \displaystyle\frac{\iiint {i_b(x,y,t).dx.dy.dt}}{A} $ ; en pratique on se contente en général de faire la moyenne des hauteurs d'eau mesurées sur les différents pluviomètres présents sur le bassin versant (éventuellement en les pondérant par une surface).
Détermination des paramètres dans le cas où l'on dispose de mesures
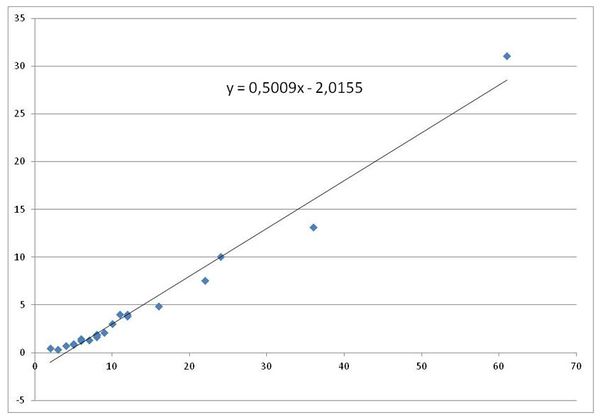
Si l'on dispose de mesures simultanées de pluie et de débit à l'exutoire du bassin versant, il est possible de tester l'adéquation statistique du modèle linéaire très simple $ (6) $ aux observations. Si le modèle est adéquat, les paramètres $ a $ et $ b’=b/a $ de l'ajustement (figure 1) donneront les valeurs moyennes du coefficient de ruissellement $ CV_A $ et des pertes initiales $ PI_A $. Si l'on ne souhaite pas introduire le terme correspondant aux pertes initiales, il suffit d'imposer la valeur $ b=0 $.
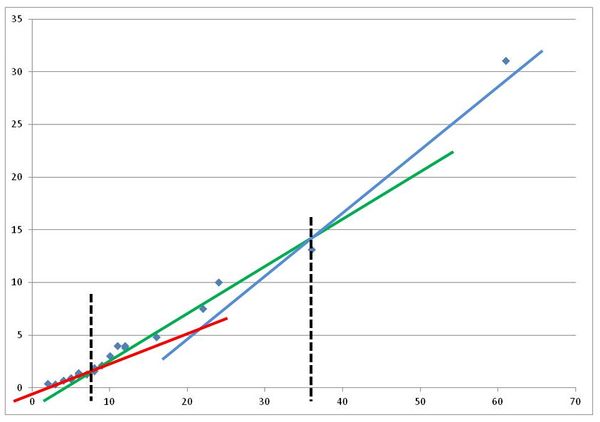
En pratique, dans la plupart des cas, on observe que la courbe n'est pas vraiment linéaire et que le coefficient global de ruissellement a tendance à augmenter avec la hauteur totale de pluie. Il est ainsi possible de considérer des ajustements différents (valeurs différentes des coefficients $ a $ et $ b $) par classe de pluies (voir figure 2).
Nota 1 : Dans ce cas, seules les valeurs de $ a $ et $ b $ associées aux pluies les plus faibles peuvent effectivement être associées à une perte initiale et à un coefficient de ruissellement.
Nota 2 : Les campagnes de mesures sont généralement courtes (de quelques mois à quelques années). Donc, même si on dispose généralement de suffisamment de données pour ajuster correctement les valeurs correspondant aux pluies faibles, voire moyennes, le nombre de pluies fortes, et encore plus, de pluies très fortes, est presque toujours insuffisant pour réaliser un tel ajustement statistique. Il est alors nécessaire d'utiliser les méthodes décrites dans le § suivant.
Évaluation des paramètres dans le cas où l'on ne dispose pas de mesures locales
Dans beaucoup de situations on ne dispose pas de mesures, ou en tous cas on ne dispose pas de suffisamment de mesures, et il est alors nécessaire d'évaluer les paramètres $ Cv_A $ et éventuellement $ PI_A $ en fonction des informations disponibles.
Évaluation du paramètre PIA
Même si ce paramètre n'est pas très important pour les pluies fortes, son évaluation correcte est nécessaire dès lors que l'on s'intéresse à des pluies faibles ou moyennes. Chocat (1978) a proposé de relier les pertes initiales à la pente moyenne du bassin versant et à la nature des surfaces par des relations linéaires de la forme :
Avec :
- $ I $ : pente du bassin versant en %.
Le tableau de la figure 3 indique des valeurs proposée pour $ a $ et $ b $ selon la pente et la nature du sol.
Si on comprend les pertes initiales comme la hauteur de pluie nécessaire au début du ruissellement, ces valeurs semblent surestimer les pertes initiales pour les petites pluies. Certaines surfaces (toits en pente, surfaces imperméables situées à proximité immédiate des avaloirs par exemple) commencent en effet à produire du ruissellement pour des hauteurs d'eau plus faibles.
Évaluation du paramètre CvA
Ce paramètre est le plus important, particulièrement pour les pluies fortes. C'est donc celui qu'il faut prédéterminer avec le plus d'attention.
Assimilation du coefficient de ruissellement au coefficient d'imperméabilisation
La façon la plus simple d'estimer $ Cv_A $, préconisée par l'instruction technique de 1977, consiste à considérer qu'il est égal au coefficient d'imperméabilisation $ C_{imp} $ :
Avec :
- $ A_{imp} $ : Surface imperméabilisée.
Dans un aménagement traditionnel, avec une grande partie des surfaces imperméables directement connectées au réseau, ce mode de calcul est acceptable pour les pluies moyennes à fortes (typiquement des hauteurs de pluie en quelques heures comprises entre 30 et 60mm). Il majore cependant le coefficient de ruissellement pour les pluies faibles (même en prenant en compte une perte initiale) et peut le minorer pour les pluies extrêmes pour lesquelles la contribution des surfaces perméables peut devenir importante, en particulier dans les zones péri-urbaines.
Améliorations possibles
Différentes améliorations ont ainsi été proposées (Schaake et al., 1967, Viessman t al., 1977, Kidd, 1979, Desbordes, 1987), la plupart avec des modèles de la forme :
avec :
- $ I $ : pente moyenne du bassin versant.
Les valeurs des paramètres $ a $, $ b $ et $ c $ peuvent être déterminées par des techniques d'analyse multivariable pour un ensemble de bassins versants donnés pour lesquels on dispose de mesures et ensuite généralisées à des bassins versants supposés avoir le même comportement hydrologique. Elles peuvent également être définies pour des classes de pluies particulières.
Proposition memento technique ASTEE
Par exemple, le memento ASTEE (2017) propose de distinguer le comportement du bassin versant pour les pluies courtes et intenses et son comportement pour les pluies longues, en utilisant les relations $ (10) $ et $ (10bis) $ suivantes :
- Pour les pluies courtes et intenses :
- Pour les pluies longues :
Avec :
- $ Cr_i $ compris entre 0,5 et 0,7 pour les pluies faibles, entre 0,7 et 1 pour les pluies moyennes à forte et valant 1 pour les pluies très fortes ;
- $ Cr_p $ valant 0 pour les pluies faibles et moyenne, compris entre 0,1 et 0,4 pour les pluies fortes et tendant vers 1 pour les pluies très fortes ;
- $ Ca_i $ compris entre 0,7 et 1 pour les pluies faibles à forte et valant 1 pour les pluies très fortes ;
- $ Ca_p $ valant 0 pour les pluies faibles et moyenne, compris entre 0,1 et 0,4 pour les pluies fortes et tendant vers 1 pour les pluies très fortes.
Cette approche constitue une avancée notable par rapport à la démarche consistant à choisir $ Cv_A $ égal à $ C_imp $ pour toutes les pluies. Il est cependant dommage que le tableau fourni en synthèse simplifie nettement le texte qui l'accompagne en ne retenant que les valeurs maximum des fourchettes des coefficients.
Pour aller plus loin
Malgré son intérêt, la méthode précédente n'est cependant pas totalement satisfaisante car elle repose sur différentes hypothèses, non explicitées et généralement non vérifiées :
- Hypothèse 1 : les surfaces dites imperméables sont effectivement imperméables : c'est ce qui justifie le choix d'un coefficient $ Ca_i $ égal à 1 (même pour les pluies faibles dans le tableau récapitulatif). Or les voiries, qui représentent 10 à 25 % des surfaces considérées comme imperméables, présentent en réalité une capacité d'infiltration qui varie, selon leur état, de 0,3 à 3 mm/h, c'est à dire qui est d'un ordre de grandeur voisin des intensités que l'on peut avoir pour une pluie longue et peu intense ; de même les toitures terrasses engravillonnées interceptent généralement plusieurs mm de pluie avant que le ruissellement ne commence ; si cette quantité est faible pour les pluies les plus fortes mais correspond à plusieurs dizaines de "pour-cents" des pluies les plus courantes.
- Hypothèse 2 : le sol et le réseau d'assainissement constituent les deux seuls exutoires possibles pour une goutte d'eau qui tombe sur un élément de surface donné. Cette hypothèse est également souvent fausse, une partie de l'eau peut en effet s'écouler soit vers un autre exutoire naturel (ruisseau par exemple) soit vers un espace où elle pourra se stocker puis s'infiltrer; il peut s'agir d'un ouvrage spécifiquement conçu pour cette fonction ou plus simplement d'une pelouse ou d'un parc. Par exemple une bonne partie des eaux précipitées sur les accès aux garages des maisons individuelles s'écoulent simplement vers la pelouse voisine et ne rejoignent le réseau d'assainissement que pour des pluies particulièrement intenses.
- Hypothèse 3 : l'élément de surface sait, dès le début de la pluie, quelle sera sa durée et son intensité et se comporte en conséquence! En effet, la seule façon d'obtenir un coefficient de ruissellement égal à 1 pour une pluie exceptionnelle, serait que ce coefficient soit égal à 1 dès le début de la pluie...
Le fait que ces trois hypothèses ne soient en général pas vérifiées montrent que la proposition précédente conduit encore souvent à majorer les coefficients de ruissellement, et ceci pour toutes les gammes de pluies. Ce n'est pas forcément dommageable dans le cas du dimensionnement des ouvrages car cette majoration va dans le sens de la sécurité, mais ce peut être dommageable dans le cas du diagnostic d'un réseau existant.
Pour aller plus loin il paraît nécessaire d'étudier de beaucoup plus près la façon dont les différentes surfaces urbaines sont connectées ou non au système collectif de drainage et contribuent aux écoulements selon les caractéristiques de la pluie. Ceci nécessite des études détaillées de terrain, menées à l'échelle de la ville, voire du quartier, et un couplage avec des mesures effectuées sur des bassins versants représentatifs des différentes situations rencontrées.
Nota : La notion de connexion au réseau va probablement devenir centrale dans les années à venir. On parle beaucoup de désimperméabiliser la ville, mais le principal enjeu pour maîtriser les flux, sera surtout de déconnecter le maximum des surfaces imperméables des réseaux, de préférence en gérant l'eau à la parcelle, au plus près de l'endroit où elle arrive au sol.
La notion de coefficient de ruissellement dans le cas de la gestion des eaux pluviales à la source
Dans le cas d'une gestion des eaux pluviales à la source la notion de coefficient de ruissellement perd l'essentiel de son sens et ne devrait plus être utilisée sans précaution car elle peut conduire à des raisonnement erronés.
Dans ce cas on s’intéresse en effet à ce qui se passe à l’intérieur de la surface du projet et non à ce qui en sort. Il est donc tout d'abord totalement illogique de considérer le coefficient de ruissellement de la zone aménagée. Celui-ci correspond en fait à la part du volume que la réglementation autorise à ne pas conserver sur le site, c'est à dire au complément du volume qu'il faut traiter sur le site. On voit bien que cette raison peut déjà conduire à des contresens entre différents interlocuteurs.
Cependant, même s’il est très difficile de considérer une surface élémentaire de quelques centaines de m2 comme un bassin versant, on pourrait, par analogie, définir le coefficient de ruissellement d’une surface élémentaire située à l'intérieur du périmètre du projet comme le rapport entre le volume d’eau précipitée sur cette surface et qui doit être traitée et le volume d’eau que cette surface a reçu. Cette utilisation du terme reste encore abusive et doit être maniée avec précaution pour les raisons explicitées ci-dessous.
Cas des surfaces aménagées
Les surfaces aménagées comprises dans le projet peuvent être :
- des bâtiments (en leur assimilant les surfaces couvertes, de type préaux),
- des surfaces au sol aménagées : voirie, parking, cheminements, cours, terrains de jeux, etc.
La totalité de l’eau de pluie reçue par ces surfaces doit bien évidemment trouver une destination. Trois possibilités existent :
- l’eau peut être gérée en totalité sur la surface elle-même (par exemple en mettant en œuvre un parking équipé d’une chaussée à structure réservoir), c’est la surface elle-même qui constitue l’ouvrage. Cet ouvrage doit de façon évidente prendre en compte la totalité du volume d’eau reçu. Le coefficient de ruissellement à prendre en compte est donc de 1.
- l’eau peut être gérée en totalité à l’extérieur de la surface (par exemple en mettant en œuvre un dispositif de stockage à l’exutoire d’une toiture), cet ouvrage doit prendre en compte la totalité du volume d’eau reçu (si l’on néglige les pertes initiales). Le coefficient de ruissellement à prendre en compte est donc également de 1 (même si l'ouvrage en question a une capacité limitée et doit être équipé d'une surverse).
- l’eau peut être gérée en partie sur la surface et en partie à l’extérieur (par exemple en infiltrant une partie de l’eau à travers le revêtement), et en partie dans un ouvrage situé à l’extérieur. Ceci signifie formellement que l’on met en œuvre deux ouvrages. Le premier ouvrage est constitué de la surface elle-même. Il doit être dimensionné pour gérer (stocker provisoirement puis infiltrer) $ p $% du volume produit. Le second ouvrage est l’ouvrage extérieur qui doit être conçu pour gérer le volume excédentaire. Le coefficient de ruissellement global à prendre en compte est donc toujours de 1. Parler de coefficient de ruissellement pour désigner la partie du volume qui doit être transporté (et traité) à l'extérieur de la parcelle $ (1-p) $%, revient donc à introduire une dissymétrie entre l'eau traitée localement et celle qui doit être traitée dans un ouvrage externe. C'est également accepter implicitement l'idée qu'il y a un ruissellement, ce que l'on va plutôt au contraire essayer d'éviter. Ces deux idées implicites sont contradictoires avec la volonté d'une gestion locale, au plus près de l'endroit où la goutte d'eau est reçue.
Cas des surfaces de pleine terre
Les surfaces de pleine terre constituent le complément des surfaces aménagées. Ce sont des surfaces destinées à être végétalisées et qui n’oppose aucun obstacle à l’écoulement de l’eau entre la surface et la nappe phréatique. On peut donc considérer que les surfaces de pleine terre sont « auto-drainantes », c’est-à-dire capables de gérer « naturellement » (c’est-à-dire sans nécessiter aucun ouvrage) la totalité des volumes d’eau qu’elles reçoivent. Ceci correspond à un coefficient de ruissellement égal à 0.
En pratique il est nécessaire de considérer deux exceptions à ce principe.
- La définition donnée aux surfaces de pleine terre n’interdit pas, bien heureusement, de les utiliser pour installer des ouvrages de stockage-infiltration, soit en surface (noue, dépression) soit en profondeur (tranchée, puits, massif). Dans ce cas la pluie reçue directement par la surface sur ou sous-laquelle l’ouvrage est installé va bien évidemment contribuer à le remplir. Cette partie de la surface de pleine terre doit donc être prise en compte dans le calcul avec un coefficient de ruissellement égal à 1.
- Dans certains cas (sol très pentu et/ou très peu perméable), un ruissellement va apparaître dès que la capacité d‘infiltration du sol sera dépassée. Ce volume supplémentaire doit également être considéré si on veut que les ouvrages soit capables de traiter les pluies fortes. Si le volume produit s'écoule vers un ouvrage, il peut alors être cohérent de prendre en compte un coefficient de ruissellement pour ces surfaces, mais c'est le seul cas.
En résumé, la notion de gestion à la source suppose que l'on prenne en considération la totalité du volume précipitée sur la zone d'étude (quelle que soit sa taille) et que l'on définisse la destination de chacun de ses éléments constitutifs (infiltration, évapotranspiration, écoulement vers un exutoire extérieur).
Conclusions
La modélisation de la fonction de production par de simples coefficients de ruissellement (ou de perte) moyens, à l'échelle d'un bassin versant est très fréquente en hydrologie urbaine. Elle n'est cependant cohérente, au regard de la fonction de transfert, que si cette dernière traduit un processus linéaire non distribué dans l'espace. Ces conditions ne sont approximativement vérifiées que dans les cas, assez fréquents cependant, de bassins versants urbanisés de petite taille, d'occupation des sols homogènes et de surfaces actives peu variables au cours d'une averse, ou d'une averse à l'autre, soumis à des précipitations relativement importantes. Dans les autres cas, l'utilisation de coefficients de ruissellement n'aura que peu d'intérêt, car elle s'éloignera de la réalité physique des processus de production et de transfert du ruissellement.
De plus cette notion n'a de sens que si l'on distingue explicitement des surfaces productrices constituant un bassin versant et un ouvrage, situé à l'aval, qui reçoit les eaux provenant de ces surfaces. Cette distinction entre surface productrice et ouvrage s'estompe dans le cas d'une gestion à la source des eaux pluviales et l'utilisation de la notion de coefficient de ruissellement (ou de coefficient d'apport) peut alors être à l'origine de malentendus. Il est donc préférable d'éviter l'utilisation de ce terme dans cette situation.
Bibliographie :
- ASTEE (2017) : Mémento technique 2017 ; téléchargeable sur : https://www.astee.org/publications/memento-technique-2017/
- Chocat,B. (1978) : Un modèle de simulation des écoulements dans les réseaux d'assainissement pluvial ; thèse Docteur ingénieur ; INSA Lyon ; 304p.
- Desbordes, M. (1987) : Contribution à l'analyse et à la modélisation des mécanismes hydrologiques en milieu urbain ; thèse d'état ; université de Montpellier ; France ; 242 p.
- Kidd, C.H.R. (1979) : Rainfall runoff process over urban surfaces ; Wallingford Institute of hydrology; Report 53 ; 84 p.
- Schaake, J.C., Geyer, J.C., Knapa, J.W. (1967) : Experimental evaluation of rational method ; journal of the Hydraulics division ; vol 93 ; HY6 ; pp 353-370.
- Viessman, W.V., Knapp, J.W., Lewis, G.I., Harbaugh, T.E. (1977) : Introduction to hydrology ; Ed. Harper and Row ; New-York ; 1977 ; 704 p.
 S'abonner à un flux RSS
S'abonner à un flux RSS