Défluence (HU)
Traduction anglaise : Bifurcation, Bifurcates
Dernière mise à jour : 26/06/2025
Mot en chantier
Une défluence (on dit parfois un défluent) est un point particulier d'un réseau ou d'un système hydrographique d'où partent plusieurs branches aval (dans le sens de la pente pour un système fonctionnant à surface libre) ; on parle parfois de bifurcation dans le cas d'une défluence avec deux branches aval.
Sommaire |
Problème posé et différents types de défluences
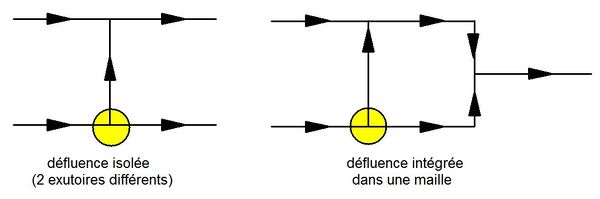
L'eau arrivant à un tel point peut emprunter différents itinéraires pour continuer son cheminement et le problème majeur à résoudre consiste à savoir comment la répartition va s'effectuer. Une défluence peut ou non être intégrée dans une maille selon que les cheminements vont ou non se rejoindre (figure 1).
Il existe des défluences naturelles sur les systèmes hydrographiques, par exemple lorsque les flux d'un cours d'eau se répartissent en deux chenaux autour d'une île. La plupart des défluences sont cependant d'origine anthropique. Les plus anciennes sont les prises d'eau sur un cours d'eau destinées par exemple à alimenter le bief d'un moulin. Dans ce cas il existe presque toujours un ouvrage hydraulique (seuil ou vanne) permettant de réguler le débit dérivé.
La plupart des défluences sont cependant présentes dans les réseaux d'eau modernes. Dans les réseaux de distribution d'eau, traditionnellement maillés, l'écoulement s'effectue en charge et les calculs sont relativement simples. En revanche, dans les systèmes d'assainissement, les écoulements s'effectuent à surface libre et prévoir la façon dont les flux se répartissent constitue une réelle difficulté.
Nota : La distinction entre une défluence et une confluence n'est pertinente que si l'on considère le sens d'écoulement de l'eau.
Éléments d’historique : origine des défluences dans les réseaux d'assainissement
Les réseaux d'assainissement, calqués sur les réseaux hydrographiques naturels, sont le plus souvent arborescents, c'est à dire que, à un nœud donné du réseau, on peut observer plusieurs tronçons amont mais un seul tronçon aval.
Cependant, au cours du temps, des raisons multiples ont pu amener les gestionnaires d'un réseau d'assainissement à y introduire des défluences :
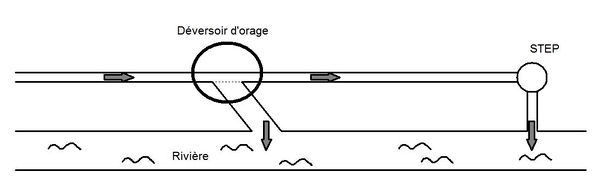
- la nécessité de délester un réseau unitaire d'une partie des flux en cas de pluie ; il s'agit alors de déversoirs d'orage (voir figure 2).
- La construction d'un nouveau collecteur, parallèle à un collecteur existant devenu insuffisant, ou permettant d'éviter une partie saturée du réseau aval (figure 3).
- Les contraintes d'exploitation ou la volonté d'assurer la permanence du service : on peut envoyer l'eau sur une branche pendant que l'on cure ou répare la seconde ; on obtient alors des schémas de réseau identiques à ceux représentés dans la figure 3.
- La volonté, en particulier à la fin du XIXème siècle, de calquer la structure du réseau d'assainissement sur celle du réseau de voirie. Dans les centres anciens des grandes villes, on trouve ainsi souvent des réseaux totalement maillés et constitués de collecteurs visitables.
Les problèmes posés par les défluences sont essentiellement liés à leur modélisation hydraulique. Il s'agit souvent de savoir comment l'eau va se répartir entre les différentes branches aval, plus rarement de connaître les risques d'ensablement dans les différentes parties du réseau.
Concepts de base et intérêt
Une défluence est donc un endroit du réseau d'où partent plusieurs tronçons. L'écoulement va en conséquence s'y partager en différents chemins qui peuvent soit se rejoindre relativement vite, par exemple derrière une pile de pont, soit diverger totalement. Un exemple extrême de ce deuxième cas est constitué par le lac d'Issarlès, en Ardèche, dont le déversoir naturel s'écoule vers le nord-ouest et rejoint la Loire, puis l'océan Atlantique, et où un deuxième déversoir artificiel a été percé pour rejoindre l'Ardèche, puis la Méditerranée.
- les défluences du premier type sont fermées et constituent des mailles, l'eau finissant par rejoindre un même point après avoir emprunté des chemins différents ;
- les défluences du second type sont ouvertes, et ne peuvent être étudiées qu'en appliquant des conditions aux limites différentes à chacune des limites aval du système (ou alors, dans le cas du lac d'Issarlès, en continuant les calculs jusqu'au détroit de Gibraltar !).
Les deux types de défluences peuvent bien évidemment coexister dans le même réseau d'assainissement.
Cette distinction, reposant uniquement sur un critère topologique, est bien sur insuffisante. En réalité, même si les deux branches aval d'une défluence se rejoignent à une distance relativement proche du point où elles se séparent, la défluence peut parfaitement être ouverte sur le plan fonctionnel. Il suffit pour cela que dans chacune des deux branches (ou même dans une seule des deux), on observe un écoulement torrentiel, même sur une longueur très courte.
Dans le cas d'une défluence fermée, les filets liquides empruntant l'une ou l'autre des branches reçoivent une information commune en provenance de l'endroit où les flux se rejoignent qui va déterminer leur répartition ; le système d'équations est donc fermé facilement.
Dans le cas d'une défluence ouverte, la fermeture du système nécessite en théorie la connaissance d'une condition à la limite dans chacune des branches, ou plus exactement de la façon dont les écoulements à l'aval de chacune des branches permettent de calculer une condition commune au droit de la défluence.
Modèles de simulation
La simulation du fonctionnement d'une défluence a pour objet principal de connaître la manière dont le débit se répartit entre les différentes branches aval et éventuellement de déterminer la forme des lignes d'eau à l'amont. Dans tous les cas, la seule équation évidente disponible est l'équation de continuité qui assure la conservation de la masse et qui se traduit généralement dans ce cas par la loi de conservation des débits (somme de tous les débits entrants égale à la somme de tous les débits sortants). Le nombre d'équations complémentaires à utiliser dépend ensuite de la formulation du problème (nombre d'inconnues). Différentes approches sont ainsi possibles.
Approche théorique
La modélisation rigoureuse du phénomène de répartition d'un fluide entre deux ou plusieurs branches aval est théoriquement possible en utilisant les équations de Navier-Stokes.
Cependant, ce type de modélisation est dans la pratique très difficile à mettre en œuvre, sauf dans des cas particuliers, pour les deux raisons suivantes :
- l'intégration de ces équations nécessite la définition précise des conditions aux limites amont et aval, c'est à dire, dans ce cas, la description complète du champ de pression et du champ de vitesse, or ces derniers sont la plupart du temps inconnus ; on est donc amené à faire des hypothèses simplificatrices (répartition hydrostatique des pressions par exemple) qui enlèvent tout intérêt à l'utilisation des équations complètes ; ceci est particulièrement vrai pour les défluences ouvertes ;
- le calcul numérique (CFD) est compliqué et nécessite la mise en œuvre de méthodes numériques puissantes, consommatrices de temps, et imposant l'utilisation de moyens informatiques appropriés ; son utilisation est possible localement sur un ouvrage mais pas sur la totalité d’un système d’assainissement.
Approche hydraulique classique
Cette approche repose sur l'utilisation des équations de Barré de Saint Venant. La première équation est issue d'une dégradation de l'équation de Navier Stokes reposant sur les hypothèses suivantes :
- tous les filets sont parallèles entre eux et parallèles au fond ;
- la répartition des pressions est hydrostatique ;
- la pente du fond est suffisamment faible pour que l'on puisse négliger la composante verticale de la vitesse.
Moyennant ces hypothèses, et en rajoutant une équation de continuité traduisant la conservation des volumes, on obtient un système d'équations différentielles qui peut être résolu numériquement sans trop de difficultés, et qui est susceptible de fournir les valeurs de vitesse et de pression (donc de hauteur d'eau) en chaque point.
Ce système est cependant insuffisant pour décrire le fonctionnement de la défluence et il est nécessaire de rajouter des équations complémentaires. La solution la plus souvent retenue consiste à considérer que les conditions limites à l'aval de chacune des branches vont se traduire par une condition simple au droit de la défluence elle-même ; on peut par exemple faire l'hypothèse :
- de la conservation de la quantité de mouvement ;
- de l'égalité des charges hydrauliques (comme dans le cas d'un réseau maillé de distribution d'eau par exemple) ;
- de l'égalité des hauteurs d'eau, c’est le choix le plus classique.
Cette méthode présente deux avantages principaux :
- elle s’intègre dans une méthode globale et (à peu près) cohérente de représentation du fonctionnement hydraulique des réseaux ;
- elle permet la représentation des inversions de sens de l'écoulement.
Elle est cependant contestable pour plusieurs raisons :
- elle repose sur des équations a priori inapplicables puisqu'elles n'explicitent pas, dans leur formulation, les forces mêmes qui conduisent l'écoulement à se séparer en deux parties distinctes (ou plus). En effet, la force de viscosité, qui a tendance à maintenir l'écoulement homogène, et les forces de frottement et d’adhérence aux parois, qui favorisent sa séparation, sont prises en compte de façon globale dans un même coefficient de rugosité ;
- elle pose un problème conceptuel majeur dans la mesure où elle nécessite d'admettre que les filets liquides sont prédestinés à choisir une direction plutôt qu'une autre alors que les conditions sont encore strictement identiques dans la section du fluide (même vitesse, même pression) ;
- son application à des défluences ouvertes (voir plus haut) impose, pour intégrer la ligne d'eau, de fixer a priori une condition à la limite aval dans chacune des branches ; le degré de liberté supplémentaire ainsi introduit n'assure plus obligatoirement l'unicité de la solution ;
- le calcul des pertes de charges singulières dues, en particulier aux changements de direction, est difficile et nécessite une description géométrique fine des ouvrages qui n'est que rarement disponible.
Malgré ces inconvénients, cette méthode est cependant utile car elle est pratiquement la seule à donner des résultats acceptables dans le cas de défluences fermées.
Approche empirique
Une troisième catégorie de modèles s'appuie sur des règles empiriques, issues de l'observation, de l'expérience ou du bon sens. Leur principe consiste à ne pas considérer la maille complète (même dans le cas de défluences fermées), mais uniquement l'ouvrage séparateur. La répartition des débits dans les différentes branches aval se fait à partir d'un critère simple, strictement local et généralement facile à mesurer ou à calculer, par exemple, proportionnellement aux pentes, aux débitances, aux débits capables, etc. Ce critère permet de bâtir des relations du type :
Avec :
- $ Qsi $: débit dans la branche aval $ i $ ;
- $ Qe $ : débit à l'amont de la bifurcation.
Les deux inconvénients principaux de ce type d'approche sont les suivants :
- incapacité à tenir compte des conditions réelles de l'écoulement dans le système d'assainissement car le critère de répartition est calculé une fois pour toute et ne peut pas être modifié ;
- absence de justification théorique (voire expérimentale dans la plupart des cas !).
Approche globale
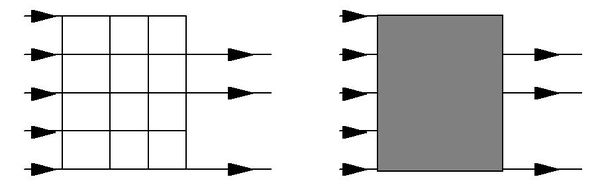
Un modèle global est un modèle qui ne s'intéresse pas au fonctionnement réel interne d'une partie maillée du réseau mais qui s'attache à bien représenter la transformation globale qu'elle fait subir à l'hydrogramme. En d'autres termes, les modèles de ce type oublient la structure interne du réseau et le considèrent comme une boite noire transformant les hydrogrammes incidents en un ou plusieurs hydrogrammes à (ou aux) exutoire(s) (figure 4).
Bibliographie :
- Carleton, M. (1985) : Contribution à l'analyse et à la modélisation du fonctionnement des déversoirs d'orage ; thèse DI - INSA Lyon ; 250 p.
- Carlier, M. (1972) : Hydraulique générale et appliquée ; Eyrolles ; Paris ; 565 p.
- Chocat, B. (1987) : Modélisation du fonctionnement des réseaux d'assainissement maillés ; rapport de recherche. ; INSA ; Lyon ; 21 p.
- Sinniger, R.O., Hager, W.H. (1989) : Constructions Hydrauliques, écoulements stationnaires ; Traité de Génie Civil de l'Ecole Polytechnique de Lauzanne ; vol. 15 ; Presses Polytechniques Romandes ; Suisse.
- Ven Te Chow (1959) : Open channels hydraulics ; Mc Graw Hill Book Company ; New York ; 600 p.
 S'abonner à un flux RSS
S'abonner à un flux RSS