Seuil hydraulique (HU)
Traduction anglaise : Weir
Dernière mise à jour : 10/04/2024
Surélévation du radier d'un ouvrage, normalement submergée, construite à des fins diverses, par exemple pour stabiliser la loi hauteur/débit au droit d'une station hydrométrique (seuil jaugeur) ou pour assurer une profondeur d'eau minimale dans un bief ou pour limiter le débit dans une direction particulière (seuil de déversoir d’orage) (voir par exemple figure 1).
Sur le plan du vocabulaire utilisé en assainissement il existe souvent une forte ambiguïté entre le mot seuil et le mot déversoir, ces mots peuvent par exemple être associés aux mêmes qualificatifs (par exemple seuil mince et déversoir à paroi mince), ou associés entre eux de différentes façons (par exemple seuil déversoir et déversoir à seuil).
Dans cet article, l'usage du mot seuil sera réservé aux ouvrages présentant la particularité physique de disposer d'une surélévation du radier qui induit une modification des conditions hydrauliques, quelles que soient les conséquences de cette modification. Les ouvrages dont la fonction est de déverser une partie du débit vers le milieu naturel, indépendamment du procédé utilisé pour contrôler le débit déversé sont traités dans l'article Déversoir d'orage.
Évolution des connaissances sur le fonctionnement hydraulique des seuils (Bonnin, 1977)
La première formule applicable aux seuils frontaux a été établie par Poleni dès 1717 :
avec :
- $ g $ : accélération de la pesanteur (m/s2) ;
- $ h_0 $ : hauteur d'eau au dessus du seuil (m) ;
- $ L $ : largeur du seuil (m) ;
- $ m $ : coefficient dépendant de la forme du seuil ;
- $ Q $ : débit au dessus du seuil (m3/s).
Les expériences de Weisbach et Francis entre 1841 et 1852, puis celles de Bazin en 1888 et enfin de Rehbock en 1912 permirent l'élaboration de formules relativement simples, applicables aux seuils frontaux. Ces formules sont d'ailleurs toujours en usage aujourd'hui. A peu près à la même époque étaient élaborées les approches théoriques sur le calcul des déversements (Belanger en 1849 ; Mullins en 1890 ; Frizell en 1899 ; Flamert en 1900 ; Boussinesq en 1907).
L'analyse du fonctionnement des seuils latéraux a pour sa part été plus tardive. La variation de la hauteur d'eau le long du seuil introduit en effet une difficulté supplémentaire. Les premiers travaux furent l’œuvre de Coleman et Smith en 1910, de Forchmer en 1924 et De Marchi en 1934 (De Marchi, 1934). Cependant, contrairement aux seuils frontaux, il ne fut pas possible d'établir une formule simple et indépendante des conditions de l'écoulement, permettant de prévoir le débit déversé en fonction de la géométrie de l'ouvrage. Ce n'est guère que dans les années 1980 que le développement des outils informatiques a permis le développement de modèles reposant sur le calcul de la ligne d'eau le long du seuil. Citons en particulier à ce sujet les travaux de Smith et El Khashab, repris ultérieurement et validé par Carleton (El Khashab & Smith, 1976), (Carleton, 1985).
Classification et concepts de base
Il existe un grand nombre de types de seuils, ayant des formes et des fonctions différentes. Plusieurs classifications sont possibles selon que l'on s'intéresse aux principes constructifs utilisés ou au mode de fonctionnement des ouvrages. On se limite souvent à une typologie fondée sur la position du seuil par rapport à la ligne principale d'écoulement. On peut ainsi distinguer :
- les seuils frontaux ;
- les seuils latéraux.
Seuils frontaux
Les seuils frontaux ont pour particularité de barrer la ligne d'écoulement sur toute sa largeur. Ils sont généralement installés plus ou moins perpendiculairement à l'écoulement (voir Figure 2).
C'est principalement sur ce type de seuil que porte cet article.
Seuils latéraux
Les seuils latéraux peuvent avoir des formes extrêmement diversifiés :
- ils peuvent être placés sur un seul côté de l'ouvrage (seuil simple) ou de chaque côté (seuil double) ;
- ils peuvent être rectilignes ou courbes ;
- leur hauteur peut être constante ou variable ;
- dans la section correspondant au seuil de déversement, la cunette d'arrivée d'eau peut avoir une section constante ou se rétrécir ;
- etc.
De plus, suivant la pente du radier, les conditions hydrauliques d'écoulement à l'amont et à l'aval, la fraction de débit déversée, etc., la ligne d'eau au dessus du seuil peut présenter différentes configurations : hauteur d'eau plus faible à l'extrémité amont du seuil qu'à l'extrémité aval ou le contraire ; ressaut à l'amont, à l'aval, au milieu ; etc.
On comprend donc que l'étude des seuils latéraux soit extrêmement difficile. Ce type de seuil étant essentiellement associé à des déversoirs d'orage, les informations relatives aux seuils latéraux sont regroupés à cet article. Nous présenterons cependant ici quelques extensions possibles des formules utilisées pour les seuils frontaux.
Modèles de simulation
Les modèles de simulation ont pour objet de décrire le fonctionnement hydraulique des ouvrages et en particulier de permettre le calcul du débit déversé pour une hauteur donnée d'eau à l'amont.
Les seuils frontaux sont théoriquement simples à étudier du fait que la ligne d'eau est parallèle à la crête du seuil. Les relations hydrauliques utilisables pour calculer le débit déversé au dessus du seuil se déduisent donc directement du théorème de Bernoulli moyennant quelques hypothèses simplificatrices. Malheureusement les conditions nécessaires au respect de ces hypothèses ne sont pas toujours vérifiées (Barbe et al., 1967) et il est souvent difficile d'analyser le fonctionnement hydraulique des ouvrages dès que leur géométrie se complique (présence d'écoulements latéraux, de vannes de fond, etc.).
Le fonctionnement des seuils est principalement déterminé par la forme de la ligne d'eau et de la section mouillée au voisinage du seuil.
Cas de base : seuil mince rectangulaire, déversement à nappe libre, sans contraction latérale
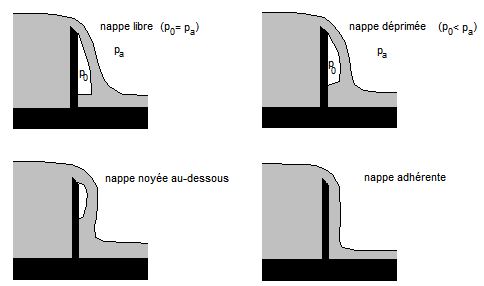
Si les dimensions de la partie du seuil qui touche l'eau sont suffisamment faibles pour être négligées, on parle de seuil à lame mince. Lorsque la nappe est suffisamment décollée du seuil pour que l'air puisse normalement circuler entre la nappe et le seuil, on dit que la nappe est libre (voir la figure 4).
Dans ce cas, et en l'absence de contraction latérale, on peut généralement faire l'hypothèse que la répartition de la pression est hydrostatique dans la lame d’eau et négliger les frottements sur le seuil. Connaissant la vitesse moyenne $ V_0 $ dans une section de référence située suffisamment à l'amont du seuil pour ne pas être perturbée par lui et suffisamment près pour que l'on puisse négliger les pertes de charge linéaires entre la section de référence et le seuil, on peut estimer la vitesse $ V $ au dessus du seuil, à une profondeur $ z $ par rapport à la surface libre de l'eau dans la section de référence, par la relation :
Le débit élémentaire $ dQ $ passant au travers d'une tranche de hauteur $ dz $ vaut donc :
avec :
- $ L $ : largeur de la tranche d'eau considérée (m).
En intégrant cette quantité entre $ z = 0 $ et $ z = h $ ($ h $ = hauteur d'eau au dessus du seuil), et en supposant que $ L $ est constant et égal à la largeur du seuil, on obtient l'expression suivante :
L'évaluation de $ h $ est délicate. En effet, $ h $ est plus faible que la différence de niveau entre la ligne d'eau dans la section de référence et le seuil, car la ligne d'eau s'abaisse au passage du seuil.
Pour résoudre ce problème, Weissbach a proposé en 1841 la relation suivante :
avec :
- $ h_0 $ : différence de niveau entre la ligne d'eau dans la section de référence et le seuil (m).
- $ μ $ : coefficient < 1, tenant compte de l'abaissement de la ligne d'eau sur le seuil et des pertes de charge.
$ V_0 $ et $ h_0 $ sont calculés en supposant que l'écoulement est permanent et uniforme. Si la vitesse de l'écoulement est faible, on peut négliger les termes en $ V_0^2 $
On retrouve alors la formule simple de Poleni :
Cette formule est cependant parfois trop restrictive, aussi Bazin a-t-il proposé de réintroduire la vitesse à l'amont, en considérant la charge totale $ H_0 $ en lieu et place de la hauteur d'eau $ h_0 $ :
avec :
- $ α $ : Coefficient sans dimension choisi empiriquement entre 0 et 1, en général $ α = 1 $.
La formule devient alors :
En pratique, on néglige cependant souvent la valeur de la vitesse et on confond les valeurs de $ H_0 $ et $ h_0 $. Différentes formules existent pour estimer $ m $ ; elles sont toutes d'origine expérimentale et ne sont donc valables que dans les conditions où elles ont été établies. Les plus connues sont récapitulées dans le tableau de la figure 3 :
Cas des nappes non libres
Lorsque la charge $ H_0 $ diminue, les filets liquides se décollent plus difficilement de la paroi du seuil, l'air a donc des difficultés à pénétrer entre la nappe liquide et le seuil. Il se forme alors une dépression sous la nappe (pression $ p_0 $ inférieure à la pression atmosphérique $ pa $). Si la différence de pression entre $ p_0 $ et $ pa $ augmente, la nappe vient se coller au seuil. La figure 4 représente les différents cas obtenus au fur et à mesure que $ H_0 $ diminue.
L'existence d'une dépression sous la nappe entraîne une augmentation du coefficient de débit. Cependant, les différentes situations présentées dans la figure 3 sont en général très instables car elles dépendent d'entrées d'air plus ou moins accidentelles entre le seuil et les filets liquides. Il n'est donc pas possible de donner une valeur de $ m $ très précise.
Cas des nappes noyées
Si le niveau de l'eau augmente à l'aval du seuil, la nappe devient noyée (voir figure 5). Il est possible de considérer que la nappe est noyée si :
Dans ce cas, Bazin propose de corriger la valeur de $ m $ par la formule suivante :
Cette formule s'applique dans le cas des seuils minces avec :
Cas des seuils épais
Selon les auteurs, les seuils sont dits épais (ou à crête large) si la hauteur d'eau au dessus du seuil à l'amont ($ h_0 $) est inférieure à 2 fois ou à 1,5 fois l'épaisseur du seuil ($ c $) (figure 6). On peut donc appliquer les règles suivantes :
- $ h_0 > 2.c $ : seuil mince ;
- $ h_0 < 1,5.c $ : seuil épais ;
- $ 1,5.c < h_0 < 2.c $ : incertitude sur le type de seuil vis-à-vis de ce critère.
Si $ c > 10.h_0 $, il n'est plus possible de considérer l'ouvrage comme un seuil et d'appliquer les formules correspondantes. Dans ce cas, il faudra considérer l'ouvrage comme un tronçon à part entière.
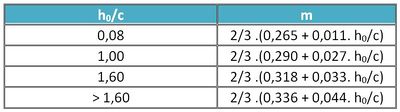
Très peu d'informations sont disponibles concernant l'effet de l'épaisseur du seuil. L'une des études les plus citées est celle réalisée par Rao et Shulka (1971). Ces auteurs proposent d'utiliser systématiquement une relation de forme identique à la relation (8) et d'exprimer le coefficient $ m $ en fonction du rapport entre la hauteur d'eau à l'amont du seuil ($ h_0 $) et son épaisseur $ c $. Le tableau de la figure 7 fournit les relations à utiliser pour différentes valeurs de $ \frac{h_0}{c} $. Pour des valeurs intermédiaires il est possible d'utiliser une interpolation linéaire.
Cas des seuils avec contraction latérale
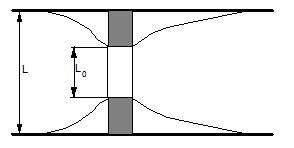
On parle de contraction latérale lorsque le seuil n'occupe qu'une partie de la section (voir la figure 8).
En pratique, la plupart des formules ont été établies pour des seuils avec des contractions rectangulaires (figure 9). Leur forme générale est la même que pour les seuils rectangulaires sans contraction, seul le calcul du coefficient $ m $ est modifié.
Citons par exemple la formule de Hegly qui s'applique aux seuils minces :
Avec :
et
Pour les seuils épais, on pourra utiliser la formule suivante [Sinniger et al., 1989] qui permet de passer d'un coefficient correspondant à un seuil mince ($ m_0 $) au coefficient correspondant à un seuil large possédant les mêmes autres caractéristiques géométriques ($ m $) :
avec
Cas des ouvrages à seuils multiples
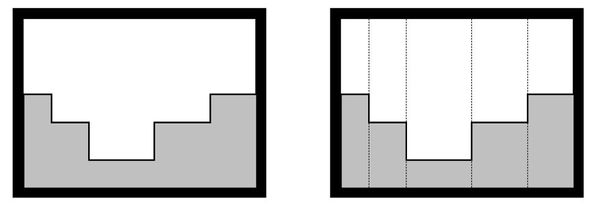
Des ouvrages constitués de plusieurs seuils situés à des hauteurs différentes sont parfois utilisés sur des rivières, de façon à permettre aux poissons migrateurs un passage facile quel que soit le débit et le tirant d’eau. Pour représenter le fonctionnement d’un ouvrage de ce type, on pourra le considérer comme l'association de plusieurs seuils rectangulaires installés en parallèle (figure 10).
Cas des ouvrages à seuil incliné
Le domaine d’utilisation de ce type d’ouvrage est le même que celui des seuils multiples. La méthode la plus simple pour traiter les seuils inclinés consiste à les décomposer en un grand nombre de seuils rectangulaires en parallèle (figure 11).
Cas des seuils triangulaires
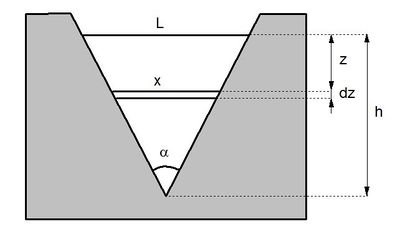
Les seuils triangulaires sont surtout utilisés en débitmétrie. Ils ont été imaginés pour permettre de mesurer, avec le même ouvrage, une gamme plus grande de débits. La section mouillée augmentant avec le tirant d’eau, le débit susceptible de s’écouler augmente donc plus vite avec la charge que dans le cas d’un seuil rectangulaire (figure 12).
Le débit $ dQ $ qui s'écoule dans une tranche de hauteur $ dz $ se met sous la forme :
En faisant intervenir l'angle $ α $ de l'échancrure, on peut écrire $ L(z) $ en fonction de $ z $ ; il est alors possible d'intégrer la relation précédente et de calculer le débit en fonction de la hauteur d'eau :
Le coefficient $ m $ dépend des caractéristiques du seuil.
On améliore parfois cette relation en lui rajoutant un terme correctif $ k_h $, destiné à tenir compte de l'influence de la tension superficielle et de la rugosité (formule de Kindsvater) :
La formule de Kindsvater est recommandée par l'Association internationale de normalisation (ISO), et le déversoir Kindsvater Shen est normalisé par l'AFNOR.
Les valeurs recommandées pour $ m $ varient de $ 0{,}58 $ à $ 0{,}62 $ selon la distance du seuil à laquelle on effectue la mesure, et pour $ k_h $ entre $ 0{,}0008 $ et $ 0{,}0022 $ mètres. Voir Seuil jaugeur (HU).
Cas des seuils latéraux
La façon la plus simple de représenter les seuils latéraux consiste à considérer que la ligne d'eau est parallèle au seuil. On obtient alors des relations dont la forme est voisine de celles utilisées pour les seuils frontaux :
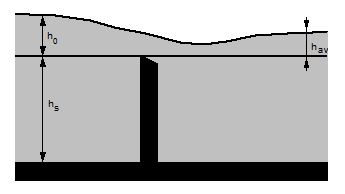
La composante latérale de la vitesse peut généralement être négligée dans le calcul de $ H $, et on peut alors admettre que $ H $ est égale à la hauteur d'eau moyenne au dessus du seuil : $ H = h $. L'évaluation de $ h $ reste cependant délicate car l'évolution de la hauteur en fonction du sens de l'écoulement dépend de plusieurs paramètres (régime d'écoulement en particulier). Certains auteurs conseillent de prendre en compte la hauteur au dessus du seuil à l'extrémité amont du seuil ($ h_0 $), d'autres à l'extrémité aval ($ h_{av} $), d'autres enfin comme la moyenne des deux. La principale difficulté est que la hauteur d'eau à l'aval du seuil dépend du débit déversé! En l'absence d'un calcul hydraulique complet, la hauteur à l'extrémité aval peut être évaluée en régime uniforme par un calcul itératif.
Pour le calcul de $ C_w $, il existe également plusieurs formules, qui font généralement intervenir $ H $ (ce qui signifie que le débit dépend d'une puissance de $ H $ différente de 3/2) ainsi que la largeur du canal ($ l_c $). Citons :
- La formule d'Engels qui s'applique dans le cas d'un écoulement fluvial sur le seuil (ligne d'eau montante : $ h_{av} > h_0 $) et pour un seuil vérifiant les conditions :
Elle considère que $ H = h_{av} $.
- La formule de Dominguez utilisable quel que soit le type d'écoulement et qui fait intervenir deux coefficients $ m $ et $ φ $ :
avec :
- $ m $ : fonction des caractéristiques du seuil et de la charge à l'amont ;
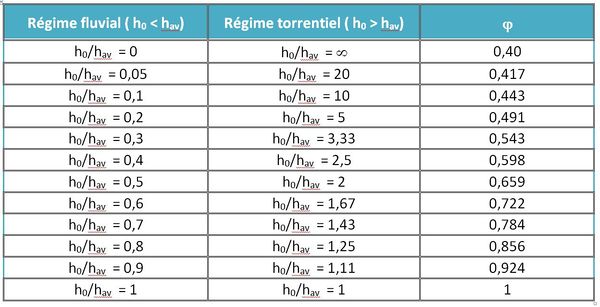
- $ φ $ : fonction du rapport $ \frac{h_0}{h_{av}} $ c'est à dire du régime d'écoulement sur le seuil.
Les valeurs de ces deux coefficients peuvent être extraites des tableaux des figures 13 et 14 suivantes.
On utilise parfois plus simplement la formule de Coleman et Smith, applicable pour un régime torrentiel ($ h_0 > h_{av} $) et qui s'écrit directement en fonction de $ h_0 $ et $ L $ :
Si la longueur du seuil est importante, il devient alors nécessaire de tenir compte de la variation de la ligne d'eau sur le seuil. Voir Déversoir d'orage latéral (HU).
Autres formes d'ouvrages
Les exemples traités dans cet article témoignent de la grande diversité des ouvrages possibles. Ils sont cependant très loin de couvrir l'ensemble des ouvrages existants dans les réseaux d'assainissement. La construction de modèles destinés à représenter le fonctionnement d'ouvrages à la géométrie encore plus complexe (seuils courbes, sauts de ski, etc.) pourra faire appel à des ouvrages généraux d'hydraulique (voir la bibliographie), voire à des études spécifiques, in situ, sur modèle réduit ou de plus en plus en utilisant des modèles 3D ; voir par exemple : http://www.graie.org/graie/graiedoc/reseaux/autosurv/REXP-AUTOSURVEILLANCE/GRAIE_2016_AnnemasseAgglo.compressed.pdf.
Bibliographie :
- Barbe A., Coulomb R., Moreau de Saint-Martin J. et Nougaro J. (1967) : Ligne d'eau et répartition du débit le long d'un déversoir d'orage latéral ; compte rendu à l'académie des Sciences de Paris.
- Bonnin, J. (1977) : Hydraulique urbaine : Ed. Eyrolles ; Paris ; 1977.
- Carleton M. (1985) : Contribution à l'analyse et à la modélisation du fonctionnement des déversoirs d'orage ; thèse docteur ingénieur ; INSA ; Lyon ; 250 p. ; septembre 1985.
- Carlier M. (1972) : Hydraulique générale et appliquée ; Eyrolles ; Paris ; 565 p.
- De Marchi G. (1934) : Saggio di teori de funzionamente degli stramazzi laterali ; L'energia electrica ; novembre 1934.
- El Khashab L. et Smith K.V.H. (1976) : Experimental investigation of flow over side weirs ; Journal of the hydraulics division ; ASCE ; vol. 102 ; HY9 ; septembre 1976.
- Lencastre A. (1961) : Manuel d'hydraulique générale ; Eyrolles.
- Rao, S.S., Shukla, M. (1971) : Characteristics of Flow over Weirs of Finite Crest Width ; Journal of Hydraulic Engineering ; disponible sur
- Sinniger R.O. et Hager W.H. (1989) : Constructions Hydrauliques, écoulements stationnaires ; Traité de Génie Civil de l'Ecole Polytechnique de Lausanne ; vol. 15 ; Presses Polytechniques Romandes ; Suisse.
Pour en savoir plus :
- Cerema : Synthèse des lois d'écoulement au droit des seuils et des déversoirs ; disponible sur sur https://www.cerema.fr/fr/centre-ressources/boutique/notice-deversoirs-synthese-lois-ecoulement-au-droit-seuils
- Vasquez, J. et al. (2006) : Guide technique sur le fonctionnement des déversoirs d'orage ; disponible sur https://www.doc-developpement-durable.org/file/eau/lutte-contre-erosion_protection-sols/Guide%20Technique%20d%C3%A9versoir%20d-orage.pdf
 S'abonner à un flux RSS
S'abonner à un flux RSS