Pluie de projet double triangle (HU)

Traduction anglaise : Double triangle design storm

Dernière mise à jour : 27/09/2022

Forme particulière de hyétogramme synthétique beaucoup utilisée en France pour dimensionner les systèmes d’assainissement pluvial.

Le concept de pluie de projet double triangle a été développé par Desbordes & Raous (1980) à partir d'une étude de sensibilité d’un modèle hydrologique (modèle du réservoir linéaire) et d’une analyse statistique d'une série chronologique de pluies réelles.

Origine du modèle

L'élaboration de ce concept repose sur un double constat :

• les événements pluvieux réels provoquant des désordres dans les réseaux d'assainissement pluvial sont généralement constitués d'une période de pluie intense relativement courte située à l'intérieur d'une séquence de pluie de quelques heures ;
• le point précédent mis à part, aucune forme particulière de distribution temporelle des intensités n'est plus probable qu'une autre.

Desbordes (1974) a donc proposé de choisir une forme particulière de pluie de projet en raisonnant, non plus par rapport au phénomène physique, mais par rapport aux éléments auxquels le modèle de ruissellement (utilisé après le modèle pluviométrique) était le plus sensible. Cette analyse de sensibilité, conduite à partir du modèle du réservoir linéaire a permis de montrer qu'une forme simple, doublement triangulaire, fournissait des formes d'hydrogrammes et des valeurs de débit maximum peu sensibles à des erreurs sur le paramètre principal du modèle de ruissellement : le lag time (Desbordes & Raous, 1980).

Formulation

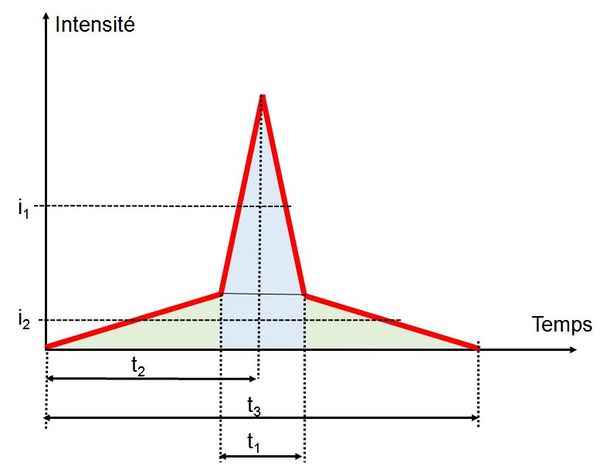
Cette pluie de projet est entièrement définie par cinq paramètres (voir figure 1) :

• la durée totale $ t_3 $ (quelques heures) ;
• la durée de la période de pluie intense : $ t_1 $ (quelques dizaines de minutes) ;
• la position de la pointe d'intensité par rapport au début de la pluie : rapport $ t_2 / t_3 $ ;
• l'intensité moyenne pendant la période de pluie intense : $ i_1 $ ;
• l'intensité moyenne en dehors de la période de pluie intense : $ i_2 $.

Figure 1 : Exemple de pluie de projet double triangle.

Les principaux éléments de choix sont les suivants :

• La durée totale $ t_3 $ peut être prise égale à 4 heures. Sur cette durée, il tombe plus de 80% de la hauteur totale des épisodes pluvieux significatifs dans 73% des cas. Par ailleurs, pour les grands bassins, sur lesquels des pluies plus longues pourraient paraître intéressantes, la variation relative du débit de pointe obtenu n'est que de 2% lorsque la durée totale de la pluie passe de deux à quatre heures.
• La durée de la période de pluie intense $ t_1 $ peut être choisie entre quinze minutes et une heure selon la nature et la surface du bassin versant étudié.
• La position de la période de pluie intense au sein de l'averse ($ θ=t_2 /t_3 $) influe de façon sensible sur le débit de pointe (le débit augmente avec $ θ $). L'analyse des pluies n'a pas permis de mettre en évidence une valeur préférentielle de $ θ $. On pourra donc prendre $ θ = 0{,}5 $, valeur moyenne, ou $ θ = 0{,}75 $ pour se placer dans une situation plus défavorable au sens des débits de pointe.
• La hauteur précipitée pendant la période de pluie intense constitue la grandeur qui influe le plus sur le débit de pointe. Sa valeur pourra être prise égale à l'intensité moyenne maximum correspondant à la même durée sur les courbes Intensité-Durée-Fréquence caractérisant la région pluviométrique et la période de retour choisies.
• La hauteur précipitée en dehors de la période de pluie intense joue un rôle moindre sur la valeur du débit de pointe. Sa valeur devra correspondre à une période de retour plus faible que celle pour laquelle on calcule le débit de pointe.

Le "guide de construction de la pluie de projet" (STU, 1986) fournit les données permettant de choisir ces paramètres.

Pluies de projet double triangle symétrique

Une analyse théorique du comportement du modèle du réservoir linéaire a conduit Chocat et al., (1981) à proposer des formules permettant de calculer directement les paramètres précédents pour une pluie de période de retour donnée. La pluie est supposée symétrique, le calcul des autres coefficients s'effectue à partir des coefficients $ a $ et $ b $ d'un ajustement de type Montana de la pluviométrie locale et d'une estimation grossière du lag time $ K $ du bassin versant à étudier. La démarche la plus simple est la suivante.

• 1- On choisit une durée de pluie intense en fonction du lag time du bassin versant à étudier

$ t_1=0{,}5.K $

• 2- On calcule la durée totale de la pluie :

$ t_3=10.t_1\qquad $ et on pose $ \qquad t_4 = t_3 - t_1 = 9.t_1 $

• 3- On calcule la hauteur de pluie précipitée pendant la période de pluie intense $ t_1 $ pour la période de retour $ T $ choisie en utilisant un ajustement de type Montana :

$ H_{max}=a(T).t_1^{b(T)+1} $

• 4- On calcule la hauteur de pluie précipitée en dehors de la période de pluie intense comme un pourcentage (de l'ordre de 80 à 90%) de la hauteur correspondant à la durée $ t_4 $ pour la période de retour $ T $ choisie en utilisant un ajustement de type Montana :

$ H_{res}=0{,}85.a(T).t_4^{b(T)+1} $

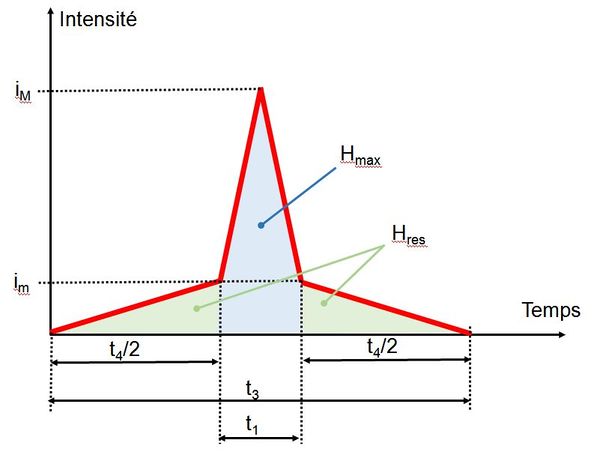
• 5- Par des considérations géométriques simples, on en déduit les paramètres constructifs $ i_m $ et $ i_M $ (Figure 2) :

$ i_m=2.\frac{H_{res}}{t_4} $

$ i_M=\frac{2.H_{max}}{t_1}-im $

Figure 2 : Signification des variables utilisées dans le mode de construction proposé.

Intérêt et limites des pluies de projet double triangle

Le principal intérêt des pluies de projet double triangle est que ce modèle peut être utilisé directement à partir des courbes intensité-durée-fréquence.

Les valeurs de débits de pointe calculées sont peu sensibles aux valeurs de $ t_1 $ et $ t_3 $. En cas d'utilisation sur un réseau drainant des bassins versants emboîtés de surfaces très différentes (ou équipés d'ouvrages de stockage), il est possible de tester une chronique de pluies de projet construites avec plusieurs valeurs de $ K $ ou directement de $ t_1 $ (par exemple $ t_1 $ = 10, 20, 30, 45, 60 minutes).

En général on utilise les pluies de projet sous une forme discrétisée. Le pas de temps de discrétisation et l'origine des temps doivent alors être choisis de façon à représenter correctement la pointe d'intensité. De façon pratique il est conseillé de retenir un pas de temps au maximum égal au 1/5 de la durée de pluie intense et de choisir l'origine des temps de façon à conserver la forme symétrique.

Nota : Discrétiser une pluie de projet double triangle est formellement équivalent à construire une pluie de projet de type Chicago.

Ce modèle, comme tous les modèles de pluie de projet, ne permet cependant pas de contextualiser l'événement et, si les enjeux sont importants, il est préférable d'utiliser des séries chronologiques de pluies observées.

Nota : Les pluies de projet double triangle sont bien adaptées pour des bassins versants dont les valeurs de lag time sont supérieures à 10 minutes. Pour des bassins versants plus petits il sera préférable d'utiliser des pluies de projet simple triangle.

Bibliographie

• STU (1986) : Guide de construction et d'utilisation des pluies de projet ; 64 p.
• Desbordes, M. (1974) : Réflexions sur les méthodes de calcul des réseaux urbains d'assainissement ; thèse Docteur ingénieur ; Université des Sciences et Techniques du Languedoc ; Montpellier ; 171 p.
• Desbordes, M. & Raous, P. (1980) : Fondements de l'élaboration d'une pluie de projet urbaine : méthodes d'analyse et application à la station de Montpellier Bel Air ; La météorologie ; n°20-21 ; pp. 317- 326 ; juin 1980.
• Chocat, B., Thibault, S., Bouyat, M. (1981) : Étude comparative des résultats fournis par la méthode de Caquot et le modèle du réservoir linéaire ; TSM l'eau ; n°7 ; pp 417-424.