Modèle distribué et modèle semi-distribué (HU)
Traduction anglaise : Distributed model and semi-distributed model
Dernière mise à jour : 07/05/2024
En hydrologie, on utilise le terme "modèle distribué" (parfois "modèle hydrologique distribué") pour désigner un modèle représentant un bassin versant par un ensemble d'éléments en interaction, chacun des éléments ayant une extension spatiale de taille suffisamment petite pour que ses caractéristiques (pente, altitude, coefficient de ruissellement, etc.) puissent être considérées comme homogènes.
Le contraire d'un modèle distribué est un modèle global.
Sommaire |
Modèles distribués et modèles semi-distribués
En pratique, il existe deux modes différents de représentation :
- Soit le bassin versant est décomposé en éléments de même nature qui échangent directement entre eux, cette décomposition étant le plus souvent faite sous la forme d'un maillage régulier de figures simples (triangles, carrés ou rectangles) (figure 1) ou parfois, en particulier dans les zones de montagne, sous la forme d'un maillage irrégulier suivant les courbes de niveau ; dans ce cas il s'agit d'un modèle distribué au sens strict ;
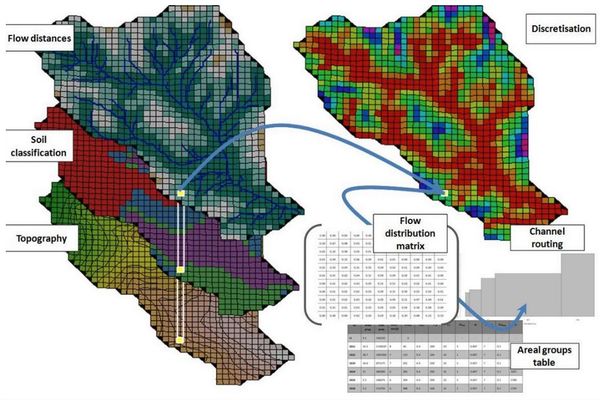
- soit la représentation du bassin versant est effectué à partir d'éléments de nature différente (figure 2) :
- des sous-bassins versants ;
- des tronçons de réseau ou de cours d'eau qui relient les sous-bassins versants à l'exutoire (ou aux exutoires) ;
- éventuellement des ouvrages spéciaux capables de modifier le fonctionnement hydrologique du système étudié.
Dans le second cas il est préférable de parler de modèle semi-distribué ou de modèle détaillé.
Il faut cependant noter que la distinction entre ces deux familles de modèles tend à s'estomper car, dans les modèles distribués, on cherche à recourir à une description de plus en plus physique des écoulements entre les mailles. On s'appuie pour ceci sur l'amélioration de la précision altimétrique des MNT et sur une diminution, éventuellement locale, de la taille des mailles (exemple de MASH, ex-AIGA). La principale limite réside dans le fait que la finesse de description du réseau hydrographique (largeur du lit en particulier) est conditionnée par la taille des mailles (voir figure 1).
Le premier mode est principalement utilisé en hydrologie générale et le second est généralement privilégié en hydrologie urbaine.
Cette différence provient principalement de la façon dont les écoulements sont organisés. Sur un bassin versant naturel ou rural, les écoulements se font en surface et le relief naturel, tel qu'il peut être décrit par un MNT, permet de bien prévoir comment les écoulements vont s'effectuer, y compris dans les thalwegs ou les cours d'eau permanents. En revanche, en milieu urbain, les écoulements sont très vite structurés par un réseau souterrain qui ne suit pas toujours, surtout à petite échelle, la pente du sol. De plus ce réseau est souvent bien connu et disponible sous la forme de SIG. Enfin, la structuration des territoires urbains en quartiers de petite taille, relativement homogènes en termes d'aménagement, également souvent bien connue, détermine fortement le comportement hydrologique du système. Il est donc plus logique d'utiliser ces informations pour décomposer le bassin versant en unités élémentaires.
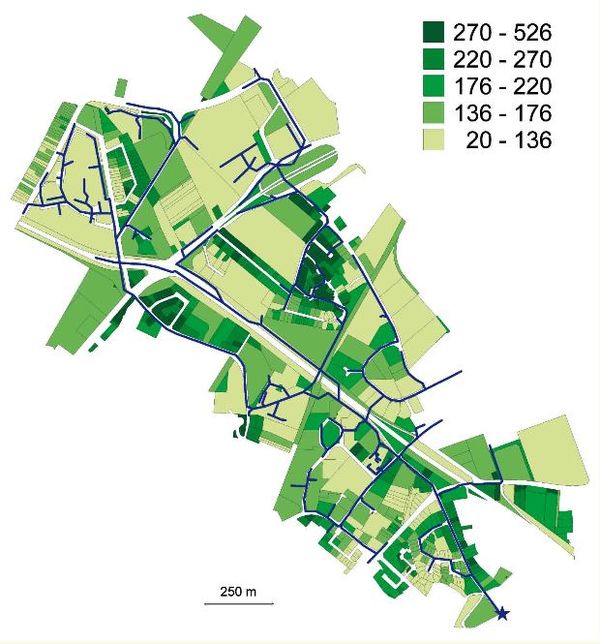
Il est cependant possible d'utiliser des modèles distribués, reposant sur un découpage en mailles régulières en zone urbaine, tout comme il est possible d'utiliser des modèles semi-distribués, reposant sur un découpage en sous-bassins versants reliés par des tronçons de réseau hydrographique, en zone rurale ou naturelle.
Ambiguïté du terme modèle
La distinction faite précédemment pointe l’ambiguïté du terme modèle qui peut représenter le système étudié et/ou la façon de représenter les phénomènes qui s'y déroulent. En effet, dans le cas d'une modélisation semi-distribué du bassin versant étudié, il devient nécessaire d'associer plusieurs familles de modèles de représentation des phénomènes : des modèles hydrologiques pour représenter le fonctionnement des sous-bassins versants (lesquels peuvent eux-mêmes être globaux ou distribués !), des modèles hydrauliques pour représenter le fonctionnement des tronçons de réseau, des modèles spécifiques pour représenter les ouvrages spéciaux conditionnant les écoulements (par exemple les ouvrages de stockage).
Intérêt et limites des modèles distribués et semi-distribués
Décomposer le système hydrologique étudié en sous-éléments de taille plus réduite présente plusieurs intérêts par rapport à une approche globale :
- pouvoir paramétrer différemment chacune des unités (mailles ou sous bassins versants) : pente, perméabilité, type d’occupation des sols ou de couvert végétal, altitude, etc. ;
- pouvoir appliquer des intensités de pluie différentes sur chacun des sous-éléments (à ce propos, dans le cas des modèles distribués, on choisit souvent des mailles carrées de 1 km de côté qui correspondent à la maille des images radars ou composites fournies par Météo-France ou d'autres) ;
- représenter spécifiquement, dans le cas des modèles semi-distribués, les écoulements dans les réseaux (qu'ils soient naturels ou artificiels comme les réseaux d'assainissement) par des modèles dont les bases physiques (hydraulique à surface libre ou en charge) sont a priori plus solides.
Il faut noter que même si les modèles distribués revendiquent la possibilité d'utiliser des modèles reposant sur une base physique pour représenter les phénomènes qui se déroulent sur chaque élément de surface, on est encore très loin d'une véritable représentation physique des différents processus. Les paramètres des modèles peuvent très rarement être évalués a priori et un calage reste toujours nécessaire.
Finesse de découpage et taille des éléments de surface
La finesse de décomposition en éléments est extrêmement variable et indépendante de la nature du modèle :
- Dans le cas d'un modèle distribué, la taille des mailles peut varier de quelques dizaines de mètres à plusieurs km ;
- dans le cas d'un modèle semi-distribué, la surface des sous-bassins versants peut également varier de quelques milliers de m2 à plusieurs milliers d'hectares.
Dans les deux cas le choix du niveau de finesse avec lequel il faut décomposer le système hydrologique étudié est délicat et dépend à la fois de sa taille et de la quantité de données disponibles.
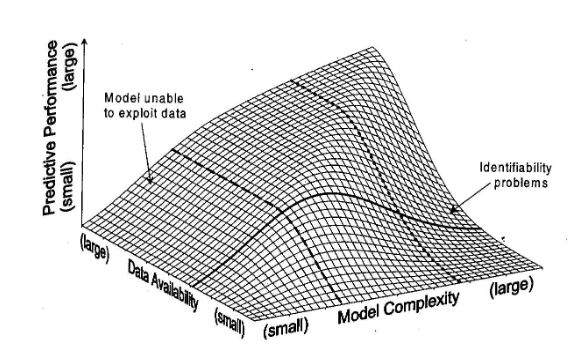
De façon assez évidente un découpage trop grossier ne permet pas d'exploiter correctement l'ensemble des informations disponibles. A l'opposé, plus on augmente la finesse du découpage et plus on augmente le nombre de paramètres du modèle. Même si certains de ces paramètres peuvent être fixés a priori de façon déterministe, d'autres dépendent nécessairement, comme indiqué plus haut, d'un calage. Si le nombre de paramètres à caler devient trop grand par rapport aux données disponibles la performance du modèle se réduit car il n'est plus possible de le caler correctement (ou plus précisément d'obtenir un calage unique).
Cette problématique est bien illustrée par la figure 3, extraite de Grayson et Blöschl (2000) qui montre qu'il existe une sorte d'optimum dans la complexité du modèle en fonction de la disponibilité des données.
La taille du système étudié est également un facteur à prendre en compte, car elle conditionne le nombre d'éléments à traiter. Par exemple, dans le cas d'un maillage à mailles carrées, diviser par 2 la longueur du coté multiplie par 4 le nombre de mailles.
Bibliographie :
- Grayson, R. et Blöschl, G. (2000) : Spatial Patterns in Catchment Hydrology : Observations and Modelling ; Cambridge University press.
- Metcalfe, P., Beven, K.J., Freer, J. (2015) : Dynamic TOPMODEL: A new implementation in R and its sensitivity to time and space steps ; 41p. ; disponible sur semanticscholar.org
- Rodriguez, F., Mosini, M.-L., Andrieu, H. (2010) : Un modèle hydrologique distribué pour les bassins versants urbains ; BLPC ; n°277 ; juillet-septembre 2010 ; disponible sur https://www.ifsttar.fr/collections/BLPCpdfs/blpc_277_43-64.pdf
Pour en savoir plus : fiche Wikhydro sur les modèles hydrologiques distribués
 S'abonner à un flux RSS
S'abonner à un flux RSS