A.07 - Incertitude dans une relation mathématique : calcul « standard »

Contexte

Quand des grandeurs (physiques ou non) sont reliées par une formule mathématique, il est possible de construire une relation entre les incertitudes associées à ces grandeurs. Le calcul standard présenté ici est particulièrement utilisé pour déduire l’incertitude associée à des mesures et détermination de grandeurs physiques.

Exemple 1. Cette approche « standard » est notamment employée dans le calcul des incertitudes de grandeurs déduites de mesures (AFNOR, 1999 ; Le Coz et al., 1999).

Définitions

Erreurs aléatoires et erreurs systématiques

Lors de l'estimation d'une grandeur (que ce soit par mesures directes ou indirectes, ou par modélisation), on distingue classiquement les erreurs aléatoires des erreurs systématiques :

• les erreurs systématiques sont indépendantes de l'opération permettant l'estimation ;
• les erreurs aléatoires varient d'une mesure à l'autre.

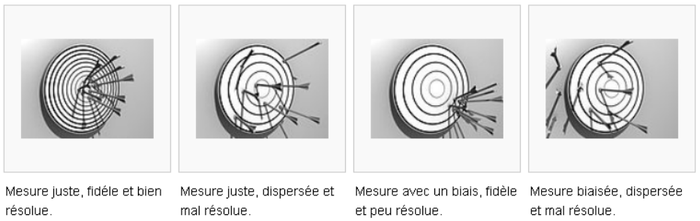
On représente classiquement les rôles respectifs des erreurs aléatoires et systématiques par une analogie avec un tir sur cible (Fig. 1), le centre de la cible représentant la valeur vraie de la grandeur à mesurer :

• si tous les impacts sont proches du centre : les erreurs aléatoires et les erreurs systématiques sont faibles ;
• si les impacts sont très étalés mais centrés en moyenne sur la cible : les erreurs systématiques restent faibles mais les erreurs aléatoires sont fortes ;
• si les impacts sont groupés mais loin du centre : les erreurs aléatoires sont faibles mais les erreurs systématiques sont fortes (biais systématiques) ;
• si les impacts sont étalés et loin du centre : les erreurs aléatoires et les erreurs systématiques sont fortes).

   Figure 1. Justesse et fidélité d'une mesure - Extrait de Rouaud 2012

Exemple 1 (suite). Lors d'une mesure, l'erreur totale Δ provient de trois types de sources qui peuvent se cumuler : Δ1 + Δ2 +Δ3 avec:

• Δ1 les erreurs systématiques correspondant au biais systématique (ou inversement à la précision ou justesse, accuracy en anglais, fiche D.03), représenté par le fait que les flèches visent bien ou non le centre de la cible de la figure 1,
• Δ2 les erreurs aléatoires ou accidentelles, généralement décrites par des lois statistiques et conduisant à la plus ou moins grande finesse de l'estimation (fiche D.04) qui traduit la dispersion (Fig. 1 : les flèches sont ou non proches les unes des autres),
• Δ3 la précision de la mesure (resolution en anglais), correspondant à la taille de la flèche sur la figure 1.

L'erreur systématique peut être connue en répétant l'opération d'estimation de la grandeur recherchée :

• pour un appareil de mesure, en l'étalonnant ;
• en modélisation, en analysant l'écart moyen entre les valeurs simulées et observées (le biais systématique).

Dans les relations présentées dans la section 2, l'incertitude correspond à la partie aléatoire des erreurs (on suppose qu'on a corrigé les estimations de façon à annuler le biais systématique).

1.2 – Incertitude absolue et incertitude relative

L'erreur absolue ΔX correspond à la différence (inconnue) entre la valeur « vraie » X d'une grandeur et son estimation (mesure ou autre) :

En l’absence d’erreurs systématiques, cette erreur (inconnue) est caractérisée par l'incertitude absolue (fiche A.01) : la valeur vraie X se trouve probablement dans (ou proche de) l’intervalle :

L'incertitude relative ou fractionnaire se définit par :

Calcul standard d'incertitude pour des variables

Les règles suivantes supposent que :

• les erreurs portant sur les variables x, y,... sont aléatoires et indépendantes ;
• la relation entre ces variables est supposée parfaitement juste (sans incertitude).

Dans ce cas, en utilisant les dérivées partielles, les relations mathématiques entre les variables se traduisent par des relations entre les incertitudes associées :

• les sommes ou soustractions se traduisent par une somme d'incertitudes absolues ;
• les multiplications ou division se traduisent par une somme d'incertitudes relatives ;
• les puissances se traduisent par un produit d'incertitudes relatives.

Exemple 2 (confluence de deux rivières). Après une confluence, le débit total est la somme des débits des affluents : . Si les débits des deux rivières sont suffisamment indépendants, l'incertitude sur le débit résultant est . À conditions hydrauliques comparables, il est donc préférable d'installer une station hydrométrique à l'aval de la confluence plutôt que de faire la somme des deux rivières amont si seul le débit résultant est recherché.

Exemple 3 (extrapolation logarithmique d'une courbe de tarage). Une courbe de tarage peut être extrapolée en hautes eaux par une relation « puissance » autour du pivot h0: où Q est le débit, h la hauteur lue à l'échelle. h0 étant fixé, la relation entre les incertitudes de débit et de hauteur (mesurée) est :

On notera que cette relation ne prend pas en compte l'incertitude sur la courbe de tarage (non négligeable, notamment en extrapolation, fiche B.09) mais traduit simplement l'impact de l'incertitude sur la mesure de hauteur « selon » cette courbe de tarage théorique.

Voir également

Fiche A.01 – Incertitude et erreur

Fiche B.09 – Incertitudes de la courbe de tarage

Fiche D.03 – Précision

Fiche D.04 – Finesse

Pour aller plus loin

• AFNOR (1999). Guide pour l'expression de l'incertitude de mesure. Norme NF ENV 13005. Indice de classement : X 07-020 ; ICS 03.120.30.

• Le Coz, J., Camemen, B., Dramais, G., Ribot-Bruno, J., Ferry, M. et Rosique, J.-L. (1999). Guide technique pour le contrôle des débits réglementaires. Guide ONEMA, Cemagref, 128 pages.

• Rouaud, M. (2012). Probabilités statistiques et analyse multicritères. Books on Demand Editions. ISBN : 978-2-8106-2461-4, 184 pages. Accessible sur http://www.incertitudes.fr/proba-stat-acp/livre.pdf (sous licence Creative Commons).

• Incertitudes expérimentales. Centre de Préparation Inter Universitaire à l’Agrégation de Physique de Montrouge. École Normale Supérieure, Universités Paris 6, Paris 7, Paris 11. Introduction au calcul d'incertitudes. TP de physique générale. EPFL

---