Réservoir linéaire (modèle du) (HU)
Traduction anglaise : Linear reservoir
Dernière mise à jour : 9/5/2020
Fonction de transfert très simple largement utilisée en hydrologie urbaine pour représenter la transformation d'un hydrogramme de pluie nette en hydrogramme à l'exutoire.
Sommaire |
Formulation mathématique
Il s’agit d’un modèle « à contrôle aval » qui repose sur l’équation de continuité (1) et sur une équation de stockage (2) :
Avec :
- $ V_s(t) $ : stockage à l’instant t ;
- $ Q_s(t) $ : débit à l’exutoire à l’instant t ;
- $ Q_e(t) $ : débit entrant ;
- $ K $ : paramètre du modèle, homogène à un temps, appelé lag time.
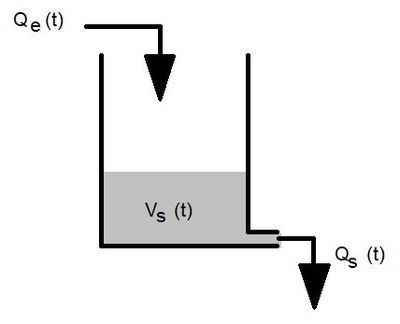
Ce modèle peut être représenté par un réservoir unique, dont la loi de stockage et la loi de vidange varient linéairement en fonction de la hauteur d'eau (voir figure 1).
La combinaison des équations $ (1) $ et $ (2) $ conduit à une équation différentielle du premier ordre, dont la solution pour $ K $ constant est :
Avec
- $ Q_s(0) $ : débit à $ t = 0 $ résultant par exemple d’un écoulement précédent ;
- $ Q_b $ : débit de base permanent éventuel.
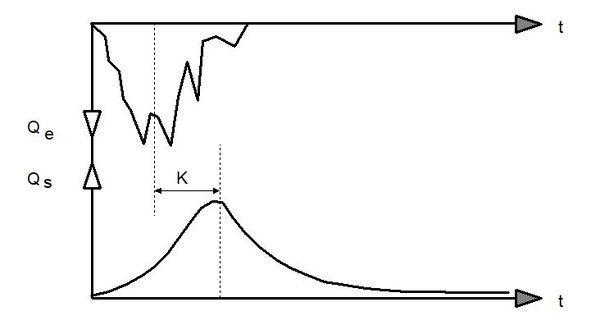
D’un point de vue théorique, le paramètre $ K $ correspond au décalage temporel des centres de gravité de $ Q_e(t) $ et $ Q_s(t) $ (voir figure 2).
Lien avec la théorie de l'hydrogramme unitaire
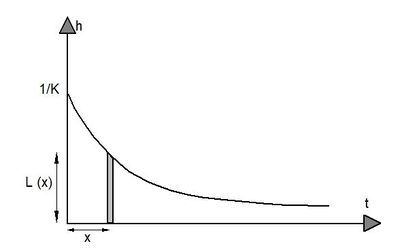
D’après l’équation (3), l’hydrogramme unitaire instantané du modèle est :
Le maximum de l’opérateur $ O(t) $ se produit à $ t=0 $ (Voir figure 3) et l’on peut donc s’attendre à ce que le modèle réponde plus rapidement que la réalité. D’un point de vue physique, l’équation de l’hydrogramme unitaire instantané est analogue à la décharge transitoire d’un condensateur électrique. C’est la raison pour laquelle le modèle agit comme un filtre « passe-bas » des pluies entrées du modèle en amortissant les composantes de hautes fréquences de ces pluies (voir figure 2).
Utilisation pratique
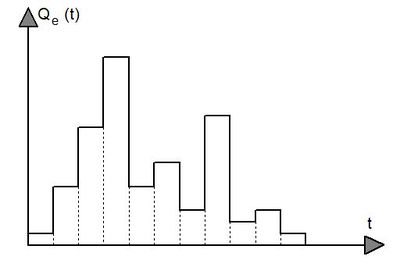
La fonction $ Q_e(t) $ n'est généralement pas connue sous une forme analytique ; elle doit donc être approchée par une fonction simple pour permettre l'intégration du modèle. La démarche la plus courante consiste à la représenter par une fonction en escalier, discrétisée sur un pas de temps constant. La figure 4 présente une telle décomposition.
Sur le plan analytique, la fonction $ Q_e(t) $ peut alors être écrite comme une succession de $ n $ segments horizontaux de droites :
$ Q_e(t) $ = $ Q_{e1} $ si $ 0 ≤ t < Δt $
$ Q_e(t) $ = $ Q_{e2} $ si $ Δt ≤ t < 2.Δt $
...
$ Q_e(t) $ = $ Q_{ei} $ si $ (i-1).Δt ≤ t < i.Δt $
...
$ Q_e(t) $ = $ Q_{en} $ si $ (n-1)Δt ≤ t < n.Δt $
Il est alors facile d'intégrer $ Q_s(t) $ :
soit finalement :
En posant $ Q_{si} = Q_{s(i.Δt)} $, on obtient ainsi une formule de récurrence facile à utiliser :
Valeur du paramètre K
De nombreuses relations empiriques ont été proposées pour déterminer le paramètre K pour des bassins versants non jaugés. En particulier, Desbordes (1974) a proposé les valeurs suivantes qui permettent de bien représenter le décalage entre les centres de gravité :
$ K = 8{,}47.A^{0,351}\quad(7) $
$ K =5{,}3.A^{0,304}.C_{IMP}^{-0,452}.I^{-0,383}\quad(8) $
$ K = 0{,}706.A^{-0,098}.C_{IMP}^{-0,512}.I^{-0,401}.L^{0,608}\quad(9) $
$ K = 5{,}07.A^{0,18}.(1 + C_{IMP})^{-1,9}.I^{-0,36}.L^{0,15}.D_p^{0,21}.H_p^{-0,07}\quad(10) $
avec :
- $ A $ : surface du bassin versant (hectares) ;
- $ D_p $ : durée de la période de "pluie critique" du bassin (de l'ordre de grandeur du temps de réponse du bassin)(mn) ;
- $ H_p $ : hauteur de pluie pendant cette durée (mm) ;
- $ I $ : pente du plus long parcours (%) ;
- $ C_{IMP} $ : coefficient d'imperméabilisation (en rapport , c'est à dire compris entre 0 et 1) ;
- $ L $ : longueur du plus long parcours de l'eau (collecteur principal) (m).
Les équations ci-dessus traduisent la représentation du paramètre K en sa qualité de durée de décalage des centres de gravité de la pluie efficace et du débit qu’elle provoque. Des travaux ultérieurs ont conduit à proposer un coefficient corrigé K’ destiné à mieux reproduire les débits observés sous la forme d’une équation. En particulier, Desbordes et Ramperez (1977) ont proposé la correction suivante :
$ K' = 0{,}7.K.A^{0,09}\quad(11) $
Ce qui conduit aux valeurs corrigées suivantes qui peuvent être utilisées au stade des projets ou des simulations de réseaux existants à condition que le bassin ne comporte pas d’ouvrages importants de stockage des eaux pluviales (bien faire attention aux unités utilisées). Nous conseillons en particulier les relations $ (14) $ et $ (15 $) qui sont les plus robustes.
$ K = 5{,}93.A^{0,441}\quad(12) $
$ K =3{,}71.A^{0,394}.C_{IMP}^{-0,452}.I^{-0,383}\quad(13) $
$ K = 0{,}494.A^{-0,0076}.C_{IMP}^{-0,512}.I^{-0,401}.L^{0,608}\quad(14) $
$ K = 3{,}55.A^{0,27}.(1 +C_{IMP})^{-1,9}.I^{-0,36}.L^{0,15}.D_p^{0,21}.H_p^{-0,07}\quad(15) $
Conclusions générales sur le modèle
Le modèle du réservoir linéaire, sous sa forme la plus simple, apparaît bien adapté à des situations assez variables allant de petits bassins versants fortement urbanisés à des bassins versants de plusieurs centaines d'hectares. La surprenante aptitude d'un modèle linéaire très simple à représenter des phénomènes complexes et fortement non linéaires semble avoir des origines multiples.
- On peut par exemple avancer que la combinaison de transformations élémentaires non linéaires, spatialement distribuées, et isolées par des singularités, peut conduire à une transformation globale approximativement linéaire. Dans ce cas, le modèle pourrait être alors physiquement adéquat du moins dans certaines conditions.
- On peut aussi penser que les bonnes performances du modèle peuvent être dues à la complexité même des systèmes urbains de collecte et d'évacuation des eaux pluviales. Les contraintes urbanistiques, techniques, financières, voire administratives, dans la réalisation des réseaux semblent en effet conduire à une certaine régularité de la géométrie des surfaces urbaines et des réseaux de collecte (Thibault, 1987).
En tout état de cause, l'utilisation de ce modèle pour simuler des bassins versants urbanisés, équipés de réseaux d'assainissement relativement développés, et dont la surface est comprise entre quelques hectares et quelques centaines d'hectares paraît totalement justifiée (O'Loughlin et al, 1996)
Bibliographie :
- Desbordes M. (1974) : Réflexions sur les méthodes de calcul des réseaux urbains d'assainissement ; thèse DI ; Université des Sciences et Techniques du Languedoc ; Montpellier ; 171p.
- Desbordes, M., Ramperez, A. ; Extension du modèle L.H.M. aux bassins versants de taille moyenne ; note L.H.M. ; Université de Montpellier ; France.
- O'Loughlin, G., Huber, W. and Chocat, B. (1996) : Rainfall-Runoff Processes And Modelling; Journal of Hydraulic Research, Vol. 34, 1996, No. 6, pp. 733-751
- Thibault S. (1979) : Eléments pour une phénoménologie en hydrologie urbaine ; thèse Docteur ingénieur ; INSA Lyon -France ; 361 p.
 S'abonner à un flux RSS
S'abonner à un flux RSS