Réservoir linéaire (modèle du) (HU) : Différence entre versions
| Ligne 2 : | Ligne 2 : | ||
Fonction de transfert très simple largement utilisée en hydrologie urbaine pour représenter la transformation d'un [[Hydrogramme (HU)|hydrogramme]] de [[Pluie nette (HU)|pluie nette]] en hydrogramme à l'exutoire. | Fonction de transfert très simple largement utilisée en hydrologie urbaine pour représenter la transformation d'un [[Hydrogramme (HU)|hydrogramme]] de [[Pluie nette (HU)|pluie nette]] en hydrogramme à l'exutoire. | ||
| + | |||
| + | == Formulation mathématique == | ||
Il s’agit d’un modèle « ''à contrôle aval ''» qui repose sur l’équation de continuité (1) et sur une équation de stockage (2) : | Il s’agit d’un modèle « ''à contrôle aval ''» qui repose sur l’équation de continuité (1) et sur une équation de stockage (2) : | ||
| Ligne 38 : | Ligne 40 : | ||
| − | Le maximum de l’opérateur <math>O(t)</math> se produit à <math>t=0</math> et l’on peut donc s’attendre à ce que le modèle réponde plus rapidement que la réalité. D’un point de vue physique, l’équation de l’hydrogramme unitaire instantané est analogue à la décharge transitoire d’un condensateur électrique. C’est la raison pour laquelle le modèle agit comme un filtre « passe-bas » des pluies entrées du modèle en amortissant les composantes de hautes fréquences de ces pluies. | + | Le maximum de l’opérateur <math>O(t)</math> se produit à <math>t=0</math> (Voir figure 3) et l’on peut donc s’attendre à ce que le modèle réponde plus rapidement que la réalité. D’un point de vue physique, l’équation de l’hydrogramme unitaire instantané est analogue à la décharge transitoire d’un condensateur électrique. C’est la raison pour laquelle le modèle agit comme un filtre « passe-bas » des pluies entrées du modèle en amortissant les composantes de hautes fréquences de ces pluies. |
| − | + | [[File:reservoir_lineaire3.JPG|400px|center|thumb|<center>''<u>Figure 3<u> : Représentation de la fonction <math>O(t)</math>.''</center>]] | |
| − | |||
| − | |||
| − | |||
| − | + | == Utilisation pratique == | |
| − | + | La fonction <math>Q_e(t)</math> n'est généralement pas connue sous une forme analytique ; elle doit donc être approchée par une fonction simple pour permettre l'intégration du modèle. La démarche la plus courante consiste à la représenter par une fonction en escalier, discrétisée sur un pas de temps constant. La figure 4 présente une telle décomposition. | |
| + | |||
| + | [[File:reservoir lineaire 4.JPG|400px|center|thumb|<center>''<u>Figure 4<u> : Discrétisation du débit à l'entrée.''</center>]] | ||
| + | |||
| + | Sur le plan analytique, la fonction <math>Q_e(t)</math> peut alors être écrite comme une succession de <math>n</math> segments horizontaux de droites : | ||
| + | |||
| + | * <math>Q_e(t)</math> = <math>Q_e1</math> si <math>0 ≤ t < Δt</math> | ||
| + | * <math>Q_e(t)</math> = <math>Q_e2</math> si <math>Δt ≤ t < 2.Δt</math> | ||
| + | * ... ; | ||
| + | * <math>Q_e(t)</math> = <math>Q_ei</math> si <math>(i-1).Δt ≤ t < i.Δt</math> | ||
| + | * ... ; | ||
| + | * <math>Q_e(t)</math> = <math>Q_en</math> si <math>(n-1)Δt ≤ t < n.Δt</math> | ||
| + | |||
| + | Il est alors facile d'intégrer <math>Q_s(t)</math> : | ||
| + | |||
| + | <center><math>formule</math></center> | ||
| + | |||
| + | soit finalement : | ||
| + | |||
| + | En posant Qsi = Qs(i.*t), on obtient ainsi une formule de récurrence facile à utiliser : | ||
| + | (7) | ||
| + | |||
| + | |||
| + | |||
| + | == Valeur du paramètre K == | ||
| + | |||
| + | De nombreuses relations empiriques ont été proposées pour déterminer le paramètre K pour ded bassins versants non jaugés. En France, on utilise généralement divers ajustements proposés par Desbordes (1974) comme, par exemple : | ||
| + | |||
| + | <math>K = 5,93.A^{0,441}</math> | ||
| + | |||
| + | <math>K = 0,494.A^{-0,0076}.IMP^{-0,512}.I^{-0,401}.L^{0,608}</math> | ||
| + | |||
| + | <math>K = 3,55.A^{0,27}.(1 + IMP)^{-1,9}.I^{-0,36}.L^{0,15}.D_p^{0,21}.H_p^{-0,07}</math> | ||
| + | |||
| + | avec : | ||
| − | + | * <math>A</math> : surface du bassin versant (hectares) ; | |
| + | * <math>D_p</math> : durée de la période de "pluie critique" du bassin (de l'ordre de grandeur du temps de réponse du bassin)(mn) ; | ||
| + | * <math>H_p</math> : hauteur de pluie pendant cette durée (mm) ; | ||
| + | * <math>I</math> : pente du plus long parcours (%) ; | ||
| + | * <math>IMP</math> : coefficient d'imperméabilisation (%) ; | ||
| + | * <math>L</math> : longueur du plus long parcours de l'eau (collecteur principal) (m). | ||
| − | Les équations de prédétermination de K | + | Les équations de prédétermination de K peuvent être utilisées au stade des projets ou des simulations de réseaux existants à condition que le bassin ne comporte pas d’ouvrages importants de stockage des eaux pluviales. |
[[Catégorie:Dictionnaire_DEHUA]] | [[Catégorie:Dictionnaire_DEHUA]] | ||
Version du 8 janvier 2020 à 14:34
Traduction anglaise : Linear reservoir
Fonction de transfert très simple largement utilisée en hydrologie urbaine pour représenter la transformation d'un hydrogramme de pluie nette en hydrogramme à l'exutoire.
Formulation mathématique
Il s’agit d’un modèle « à contrôle aval » qui repose sur l’équation de continuité (1) et sur une équation de stockage (2) :
Avec :
- $ Vs(t) $ : stockage à l’instant t ;
- $ Qs(t) $ : débit à l’exutoire à l’instant t ;
- $ Qe(t) $ : débit entrant ;
- $ K $ : paramètre du modèle, homogène à un temps.
La combinaison de ces deux équations conduit à une équation différentielle du premier ordre, dont la solution pour $ K $ constant est :
Avec
- $ Q_s(0) $ : débit à t = 0 résultant par exemple d’un écoulement précédent ;
- $ Q_b $ : débit de base permanent éventuel.
D’un point de vue théorique, le paramètre $ K $ correspond au décalage temporel des centres de gravité de $ Q_e(t) $ et $ Q_s(t) $. D’après l’équation ci-dessus, l’hydrogramme unitaire instantané du modèle est :
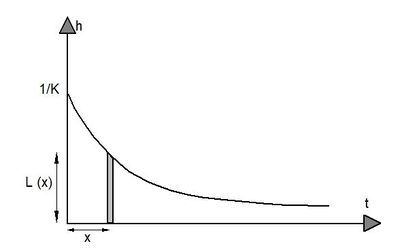
Le maximum de l’opérateur $ O(t) $ se produit à $ t=0 $ (Voir figure 3) et l’on peut donc s’attendre à ce que le modèle réponde plus rapidement que la réalité. D’un point de vue physique, l’équation de l’hydrogramme unitaire instantané est analogue à la décharge transitoire d’un condensateur électrique. C’est la raison pour laquelle le modèle agit comme un filtre « passe-bas » des pluies entrées du modèle en amortissant les composantes de hautes fréquences de ces pluies.
Utilisation pratique
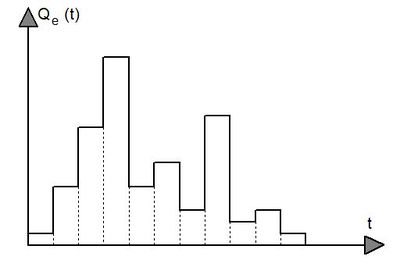
La fonction $ Q_e(t) $ n'est généralement pas connue sous une forme analytique ; elle doit donc être approchée par une fonction simple pour permettre l'intégration du modèle. La démarche la plus courante consiste à la représenter par une fonction en escalier, discrétisée sur un pas de temps constant. La figure 4 présente une telle décomposition.
Sur le plan analytique, la fonction $ Q_e(t) $ peut alors être écrite comme une succession de $ n $ segments horizontaux de droites :
* $ Q_e(t) $ = $ Q_e1 $ si $ 0 ≤ t < Δt $ * $ Q_e(t) $ = $ Q_e2 $ si $ Δt ≤ t < 2.Δt $ * ... ; * $ Q_e(t) $ = $ Q_ei $ si $ (i-1).Δt ≤ t < i.Δt $ * ... ; * $ Q_e(t) $ = $ Q_en $ si $ (n-1)Δt ≤ t < n.Δt $
Il est alors facile d'intégrer $ Q_s(t) $ :
<center>$ formule $</center>
soit finalement :
En posant Qsi = Qs(i.*t), on obtient ainsi une formule de récurrence facile à utiliser :
(7)
Valeur du paramètre K
De nombreuses relations empiriques ont été proposées pour déterminer le paramètre K pour ded bassins versants non jaugés. En France, on utilise généralement divers ajustements proposés par Desbordes (1974) comme, par exemple :
$ K = 5,93.A^{0,441} $
$ K = 0,494.A^{-0,0076}.IMP^{-0,512}.I^{-0,401}.L^{0,608} $
$ K = 3,55.A^{0,27}.(1 + IMP)^{-1,9}.I^{-0,36}.L^{0,15}.D_p^{0,21}.H_p^{-0,07} $
avec :
- $ A $ : surface du bassin versant (hectares) ;
- $ D_p $ : durée de la période de "pluie critique" du bassin (de l'ordre de grandeur du temps de réponse du bassin)(mn) ;
- $ H_p $ : hauteur de pluie pendant cette durée (mm) ;
- $ I $ : pente du plus long parcours (%) ;
- $ IMP $ : coefficient d'imperméabilisation (%) ;
- $ L $ : longueur du plus long parcours de l'eau (collecteur principal) (m).
Les équations de prédétermination de K peuvent être utilisées au stade des projets ou des simulations de réseaux existants à condition que le bassin ne comporte pas d’ouvrages importants de stockage des eaux pluviales.
 S'abonner à un flux RSS
S'abonner à un flux RSS